���V�|�R�A�^�C���R�[�i�����O�t�H�[�X�̃X���b�v�p�ɑ������`���ƃX�e�A������
�@�^�C�������̔���`���Ɋւ��ẮA�d�ɑ���R�[�i�����O�p���[�̔���`�����X�e�A�����ɗ^����e���ɂ������R�|�Q�A�d�ʔz���ƃX�e�A�����i�R�[�i�����O�p���[�̉d�ɑ������`��������ꍇ�j�����O�q���܂������A�����ł̓X���b�v�p�ɑ���R�[�i�����O�t�H�[�X�̔���`�����X�e�A�����ɗ^����e���ɂ��ĊȒP�ɏ��������Ǝv���܂��B
���~���Ă���ԗ��ɂ��ẮA�O��̃^�C�����̘͂a�Ɖ��S�͂��ނ荇���Ă��邱�Ƃ���A
�@�l�E���E���{�Q�x���{�Q�x�����O�@�@�@�@�c�i�V�|�P�j
�i���i�U�|�P�j�Ɠ����j
�����ŁA�l�F�ԗ����ʁA���F�d�͉����x�A���F����f�i�d�͉����x�̉��{�������f�ƕ\�����́j�A�x���F�O�ւP�ւ̃^�C�����́A�x���F��ւP�ւ̃^�C�����́B
�܂��A�d�S�_���̃��[�����g���ނ荇���Ă��邱�Ƃ���
�@�Q�E�k���E�x���|�Q�E�k���E�x�����O�@�@�@�@�@�c�i�U�|�Q�j
�����
�@�Q�x�����|�l�E���E�k���^�k�E���@�@�@�@�c�i�V�|�Q�j
�@�Q�x�����|�l�E���E�k���^�k�E���@�@�@�@�c�i�V�|�R�j
��L�̂����A�l�E���E�k���^�k�Ƃl�E���E�k���^�k�́A���ꂼ��O���d�ƌ㎲�d�ł��邩��A�x���Ƃx���͂��ꂼ��։d�����i����f�F���f�ƕ\�����́j�����������̂Ɠ������Ȃ�܂��B���������Ƃ�₱�����ł����A�v����ɂO�D�T�f�Œ��~���Ă���Ƃ��̑O���E�֍��v�̃^�C�����͂��A���E�֍��v�̑O�։d�Ŋ���O�D�T�ɂȂ�A��ւ̉��͂̍��v����։d�̍��v�Ŋ���O�D�T�ɂȂ�Ƃ������Ƃł��B
�@�������}7.5�̂悤�ȃX���b�v�p�ɑ���^�C���R�[�i�����O�t�H�[�X�̓������l���܂��B�A���c���̓R�[�i�����O�t�H�[�X���̂��̂ł͂Ȃ��։d�Ŋ����Ė����������Ă��܂��B����͐���f�Ɠ���Ɉ�����悤�ɂ��邽�߂ł��B
![]()
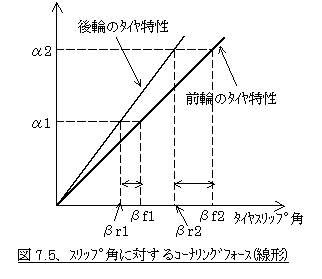
�@���̗�ł̓R�[�i�����O�t�H�[�X�i��։d�Ŋ��������́j�̓X���b�v�p�ɑ��Đ��`�ł��B����O�ւ̓����ƌ�ւ̓������d�Ȃ��Ă��܂���B����͗Ⴆ�ΑO�q�����t�����g�̏d���ԂȂǂ̗�ŁA�O�ւ̃R�[�i�����O�t�H�[�X����ւ��d���O�։d�قǂɂ͑傫���Ȃ����Ƃ������Ă��܂��B�v����ɉd�ɑ���R�[�i�����O�p���[�̔���`���������ł����A�X���b�v�p�ɑ���R�[�i�����O�t�H�[�X�͐��`�ł��B
�@���A���̎ԗ������P�f�Œ��~���Ă���Ƃ���ƁA���̂Ƃ��̑O��ւ̃^�C���X���b�v�p�́A�}��������P�A�����P�A�܂��A���Q�f�̂Ƃ��͂��ꂼ������Q�A�����Q�ƂȂ�܂��B
�@���āA���Q�|�Q�A�O��փ^�C���X���b�v�p�ƃX�e�A�����̊W�@���̍����v���o���Ă��������B���~���Ă���ԗ��͉��������藧���Ƃ�������܂����B
�@���k�^�q�{�����|�����@�@�@�@�c�i�V�|�S�j
�@�i���i�Q�|�Q�j�̕ό`�j
�i�����ŁA�F�O�֎��NJp�A�k�F�z�C�[���x�[�X�A�q�F���a�A�����F�O�փ^�C���X���b�v�p�A�����F��փ^�C���X���b�v�p�j
�܂��A�����|�������O�ł���A���_�[�X�e�A�ł��邱�Ƃ��������܂����B
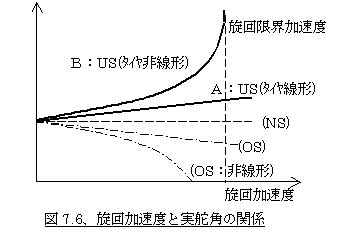
�}7.5�̗�͂����������x�Œ��~���Ă���Ƃ��̃����A�����̊W�������|�������O�ƂȂ��Ă���̂ŃA���_�[�X�e�A�̎ԗ��ł���Ƃ����܂����A���̓��������`�ł��邽�߁A��������x���グ�Ă����ƃ����|���������̊����ő����Ă��������ł��邱�Ƃ��킩��܂��B�܂莮�i�V�|�S�j����A��������x���グ�Ă����Ǝ��NJp�i�ȒP�ɂ̓n���h���NJp�ƍl���Ă��悢�j�����̊����Ő葝���Ȃ���Ȃ�Ȃ��ԗ��ƌ������Ƃł��B���̂��Ƃ��������x�ɑ�����NJp�̃O���t�ŕ\���ƁA�}7.6���̂`�̂悤�ɂȂ�܂��B
 |
�����ł����X���b�v�p�ɑ���^�C���R�[�i�����O�t�H�[�X����������`�������ꍇ�͂ǂ��Ȃ邩�l���Č��܂��傤�B���ۂ̃^�C���ł͕K�����̂悤�Ȕ���`����L���Ă���̂ł��B
��ʓI�Ƀ^�C�����}7.7�̂悤�ɃX���b�v�p�𑝂₵�Ă����Ă�����قǂɂ̓R�[�i�����O�t�H�[�X���傫���Ȃ炸�A���ɂ͂���l�œ��ł��ɂȂ��Ă��܂����Ƃ����V�|�Q�A�^�C�����͂̔���`���̗��R�ɂ��ā��̍��Ő������܂����B
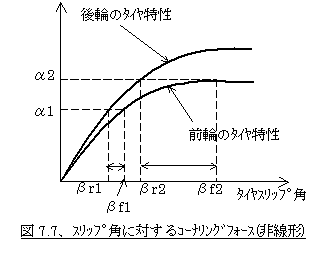 |
���̏ꍇ�͐}���疾�炩�Ȃ悤�ɐ�������x���グ�Ă����ƃ����|�������ǂ�ǂ�傫���Ȃ�A���ɂ͖�����ƂȂ��Ă��܂��܂��B������������x�ɑ�����NJp�̃O���t�ŕ\���ƁA�}7.6���̂a�̂悤�ɂȂ�܂��B�܂���NJp�͐�������x���グ�Ă����Ƃǂ�ǂ�傫���Ȃ�A���ɂ̓t���]�ǂ��Ă��Ԃɍ���Ȃ��Ȃ�A�Ƃ������Ƃł��B���A���̂悤�ȏ�Ԃ��u�t�����g�h���t�g�A�E�g�v�ƌ����A���̂Ƃ��̐�������x���u�ő��������x�v�ƌ����܂��B����͂�������Ă���������x���グ�邱�Ƃ��ł����A��ΐ�قǃ^�C�����͂̎ԑ̑O�㐬�����傫���Ȃ��Ă��܂��A���s��R�ɂȂ����Ƃ�����Ԃł��B
�@�]�k�ł����A���S�Ȏԗ������ɂ͂��́u�ő��������x�v���Ȃ�ׂ����߂�Ƃ������Ƃ��K�v�ł����A�����Ɏ�������i�}7.6���a���j���Ȃ�ׂ��Ȃ��炩�ɁA�h���C�o�[�ɗ\�����₷�������ɂ��邱�Ƃ����߂���̂ł��B
�����̍��ڂց��@�@���ڎ��ց��@�@���g�n�l�d�ց�