<7−4、ニューマチックトレールとセルフアライニングトルクについて>
ところで、タイヤ横力が発生しているときその着力点はどこなのかということについては今まで触れてきませんでした。ここでいう着力点とは、力を一点に代表したときどのポイントに働いているかということです。ヨーイングモーメントの計算式なども横力はタイヤ接地中心に働くものとして書いていますが実際には若干異なり、スリップ角の小さい領域では普通接地中心より数十mm後になります。接地中心からこの横力の着力点までの距離をニューマチックトレールといいます。
車両のヨーイングモーメントなどの比較的マクロな問題の場合はニューマチックトレールを無視して考えても支障ないのですが、次章で出てくるコンプライアンスステアなどを考える場合は問題とする長さのスケールが小さくなるので無視できなくなってきますので、ここで簡単に説明しておきます。
といっても新しいことを考える必要はなく、今まで見てきたタイヤ横力の発生モデルに沿ってその力の中心がどこにあるかを考えればよいわけです。<7−1、タイヤ変形のモデルによる横力の説明>のところでも説明したようにスリップ角の付いたタイヤのトレッドゴムの変形は図7.2のように三角形のような形になります。
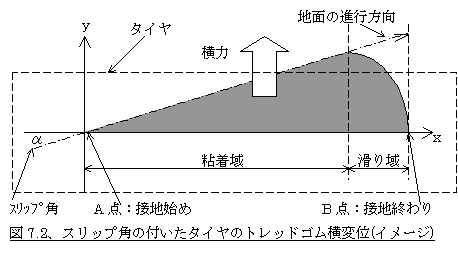
この変形の形がすなわち横力の分布の形ですから、横力の着力点(横力を一点に代表したときどのポイントに働いているか)はこの三角形の面積の重心が接地長の中のどの位置にあるかを考えればよいということになります。一見してもその形から重心は真ん中より右寄りにありそうです。真ん中が接地中心ですから、右よりということは接地中心より後ということです。しかし、どれくらい後にあるのでしょうか。簡単に計算してみましょう。
いまスリップ角が微少だとするとトレッドゴムの変位は摩擦限界を超えていないので滑り域は無視できるほど小さくなります。すると三角形は底辺を接地長とする直角三角形に近似できます(図7.8参照)。
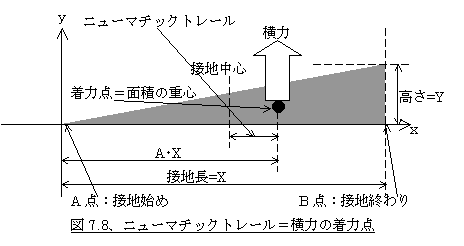
この直角三角形の面積の重心はどこにあるでしょうか。接地長をX、最大変位(三角形の高さ)をY、重心の接地前端からの距離をA倍のXとすると、接地前端から重心までの直角三角形の底辺はA・Xで高さはA・Yとなり、その面積は全体の面積の半分だから、
A・X×A・Y/2=X・Y/4 …(7−5)
よって
A2・X・Y=X・Y/2
これから
A2=1/2、 A=√2/2≒0.7
となります。すなわち重心は接地前端から接地長の7割程度後方、つまり接地中心からは2割程度後方ということがわかります。接地長が150mm程度だとすれば、ニューマチックトレールは約30mm程度ということになるわけです。
ちなみにスリップ角が大きくなってくると<7−2、タイヤ横力の非線形性の理由について>の項で説明した理由により三角形の頂点が次第に接地前端の方に寄ってきます。したがって面積の重心も接地前端に寄ってくるのでニューマチックトレールは次第に減少してきて、ついには負の値(接地中心よりも前方)となります。
ところで、スリップ角が比較的小さいとき横力の着力点が接地中心より後方にあるということは、そのニューマチックトレールを腕の長さとする接地点回りのモーメントがスリップ角を戻す方向に発生しているということです。このモーメントをセルフアライニングトルク(SAT)といいます(図7.9参照)。
 |
セルフアライニングトルク(SAT)=接地点回りのモーメント=横力×ニューマチックトレール
つまりスリップ角が付いて横力を発生しているタイヤはそれ自身でスリップ角=0の状態に戻ろうとするモーメント(トルク)を発生しているのです。ハンドルを切って旋回している状態からハンドルを離すと直進状態に戻っていく主な要因は、このセルフアライニングトルクと「タイヤ横力×キャスタートレール」(正確には各々に「cosキャスター角」をかけたもの)のモーメントがキングピン回りに働くためです。ここでキングピンとはタイヤの転舵方向の回転軸のことで、キャスタートレールというのはキングピンを延長して地面にぶつかったポイントとタイヤ接地中心の車両前後方向の距離のことです(図7.10参照)。
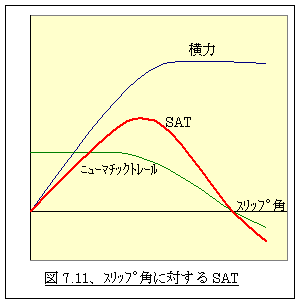
ちなみにスリップ角に対するセルフアライニングトルクは、スリップ角が小さい領域では横力の上昇にしたがって増加し、スリップ角が大きくなってくると次第にニューマチックトレールが短くなってくるため減少して、スリップ角が非常に大きい領域では負の値にもなる、図7.11のような形になります。
 |