亙俈亅俀丄僞僀儎墶椡偺旕慄宍惈偺棟桼偵偮偄偰亜
丂慜崁傪摜傑偊偰丄嘆壗屘僗儕僢僾妏偑戝偒偔側傞偲墶椡乮偁傞偄偼僐乕僫儕儞僌僼僅乕僗乯偼僒僠儏儗乕僩偡傞乮弮憹偟側偄乯偺偐丠偲丄嘇壗屘椫壸廳傪戝偒偔偟偰偄偭偰傕墶椡乮僐乕僫儕儞僌僷儚乕乯偼弮憹偟側偄偺偐丠偵偮偄偰峫偊偰傒偨偄偲巚偄傑偡丅
嘆丄僗儕僢僾妏偑彫偝偔杸嶤椡偑乽僩儗僢僪崉惈亊僩儗僢僪偺嵟戝曄埵乿傪忋夞偭偰梋桾偺偁傞忬懺偱偼妸傝堟偼柍帇偱偒傞傎偳彫偝偔丄僩儗僢僪慡懱偺曄埵偼偪傚偆偳捈妏嶰妏宍偺傛偆側宍偵側傝傑偡丅偙偺斖埻偱偼僗儕僢僾妏偺憹戝偵偮傟偰嵟戝曄埵検傕憹偊偰丄捈妏嶰妏宍偺崅偝偑扨弮偵憹偊傞僀儊乕僕偲側傝墶椡偑憹偊傑偡丅偟偐偟乽僩儗僢僪崉惈亊僩儗僢僪偺嵟戝曄埵乿偑杸嶤椡傪忋夞偭偰偟傑偆傛偆側僗儕僢僾妏椞堟偱偼曄埵検偑尷奅偲側傞億僀儞僩乮偡側傢偪擲拝堟偲妸傝堟偺嫬奅乯偑懚嵼偟丄僗儕僢僾妏傪偦傟埲忋戝偒偔偟偰傕僩儗僢僪偺嵟戝曄埵偼戝偒偔側傜偢丄扨偵偦偺億僀儞僩偑憗偔側傞偩偗偱偡乮恾7.4嶲徠乯丅
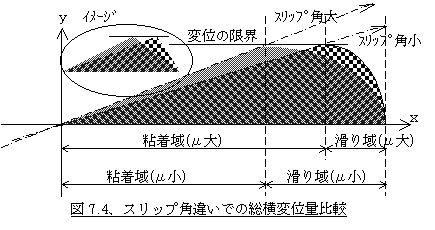
丂妸傝堟偺曄埵検傪榑偢傞偺偼擄偟偄偺偱懡彮峳偭傐偄偱偡偑丄僩儗僢僪偺墶曄埵慡懱偺宍傪丄曄埵偺尷奅揰傪捀揰偲偡傞嶰妏宍偲嬤帡偡傟偽丄偦傟埲忋僗儕僢僾妏傪憹傗偟偰傕曄埵偺捀揰偺埵抲偑愙抧慜抂偵嬤偯偔偩偗偱捀揰偺崅偝偼曄傢傜側偄丄偡側傢偪乽掙曈亊崅偝乛俀乿偑曄傢傜側偄丄廬偭偰戝偞偭傁偵尵偆偲僞僀儎墶椡偑偝傎偳憹偊側偄偲偄偆偙偲偵側傝傑偡丅
偪側傒偵僐乕僫儕儞僌僼僅乕僗偼偙傟偵壛偊偰偦偺掕媊偐傜僗儕僢僾妏暘偩偗嵗昗曄姺偟偨抣乮偡側傢偪墶椡亊們倧倱兛乯偲側傞偨傔丄們倧倱兛偑兛偺憹戝偵敽偭偰尭彮偡傞暘峏偵彫偝偔側傝傑偡丅墶椡亊倱倝値兛暘偼憱峴掞峈乮僐乕僫儕儞僌掞峈乯偲側傝傑偡丅偙傟偑傛偔僪儔僀價儞僌僗僋乕儖側偳偱嫵偊傞乽僴儞僪儖傪愗傝偡偓傞偲乮慜椫偺僞僀儎僗儕僢僾妏傪憹傗偟偰傕乯懬偑岠偐側偄乮僞僀儎墶椡偑憹偊側偄乯乿椞堟偲偄偆傢偗偱偡丅
嘇丄椫壸廳傪戝偒偔偟偰偄偭偰傕墶椡乮僐乕僫儕儞僌僷儚乕乯偼弮憹偟側偄棟桼偼娭楢偡傞梫慺偑懡偔丄嘆傎偳扨弮偱偼側偄偲巚傢傟傑偡丅僗儕僢僾妏偑戝偒偄椞堟偼嘆偺愢柧偑偁傞偺偱丄偙偙偱偼壸廳偺塭嬁偼僗儕僢僾妏偺旝彮側椞堟偱峫偊側偔偰偼側傝傑偣傫丅偙偺椞堟偱偼丄側偍偐偮椫壸廳偺彫偝偄椞堟偱偼丄壸廳偵懳偟偰墶椡乮偁傞偄偼僐乕僫儕儞僌僷儚乕乯偼傎傏斾椺偟偰憹壛偡傞偙偲偑曬崘偝傟偰偄傑偡丅偙傟偼愙抧挿偺擇忔偑壸廳偵斾椺偟偰憹壛偡傞偨傔偲峫偊傜傟偰偄傑偡丅偳偆偟偰愙抧挿偺擇忔偑壸廳偵斾椺偟偰憹壛偡傞偲墶椡偑壸廳偵斾椺偡傞偐偲偄偊偽丄堦斒揑偵旝彮僗儕僢僾妏丄掅壸廳乮偁傑傝愙抧挿偺挿偔側偄忬懺乯偱偼妸傝堟偑傎偲傫偳柍偄偨傔僩儗僢僪柺偺墶曄埵検偼乽愙抧挿乮亖掙曈乯乿亊乽愙抧挿亊倱倝値兛乮亖崅偝乯乿乛俀偺捈妏嶰妏宍偺柺愊偱嬤帡偱偒傞偲峫偊傑偡丅偙偺幃偼乮愙抧挿偺擇忔亊倱倝値兛乯偱偁傞偨傔丄愙抧挿偺擇忔偑俀攞偵側傟偽墶椡傕俀攞偵側傞偲偄偆傢偗偱偡丅偲偙傠偑壸廳偑憹戝偟愙抧挿偑旕忢偵挿偔側偭偰偔傞偲丄乽愙抧挿亊倱倝値兛乿偑旕忢偵戝偒偔側偭偰兪偲掁傝崌偆曄埵傪墇偊丄妸傝堟偑柍帇偱偒側偄傎偳戝偒偔側偭偰偒傑偡丅梫偡傞偵嶰妏宍偺崅偝偑乽愙抧挿亊倱倝値兛乿偲崌抳偟側偔側傞傢偗偱偡丅乮棟桼偼尩枾偵偼偙傟偩偗偱偼偁傝傑偣傫偑乯偙傟傜偵傛傝墶椡乮偁傞偄偼僐乕僫儕儞僌僷儚乕乯偑弮憹偟側偔側偭偰偔傞偲峫偊傜傟偰偄傑偡丅
丂彯丄僞僀儎嬻婥埑偺塭嬁偵偮偄偰偼丄崅壸廳堟偱偼嬻婥埑偑掅偄曽偑墶椡偑壓偑傝丄掅壸廳堟偱偼媡偵嬻婥埑偑崅偄曽偑墶椡偑掅偔側傞孹岦偑偁傞傛偆偱偡丅偙偺棟桼偼丄崅壸廳堟偱嬻婥埑傪壓偘傞偲峏偵愙抧挿偑挿偔側傝丄愭掱壸廳偺塭嬁偱弎傋偨棟桼偑傛傝尠挊偵側傞偨傔丅傑偨丄掅壸廳堟偱媡偺孹岦偲側傞偺偼丄掅壸廳堟偱嬻婥埑傪忋偘傞偲愙抧挿偑嬌抂偵抁偔側傝丄杸嶤椡偵梋桾偑偁傞偺偵扨弮偵嶰妏宍偺柺愊偑庢傟側偔側傞偨傔乮娙扨偵尵偆偲愙抧柺愊偑彫偝偔側傝偡偓傞偨傔乯偲峫偊傜傟傑偡丅