���Q�|�Q�A�O��փ^�C���X���b�v�p�ƃX�e�A�����̊W�@��
�@�O�q�̊T�O�I�������A�}��p���Ă��������ڂ������Ă݂܂��傤�B
�ŏ��ɐ���~��ɒ�~���Ă���ԗ��̗l�q�ƁA���鑬�x�������Đ��Ă���ԗ��̗l�q��}�Ŏ����A��������O�փX���b�v�p��������ь�փX���b�v�p�����ƁA�X�e�A�����̊W������������Ǝv���܂��B
�@�}2.3�͂�����a�ɂ҂���ƍ��킹�ĎԂ��~�������Ƃ��̂悤����\���Ă��܂��B
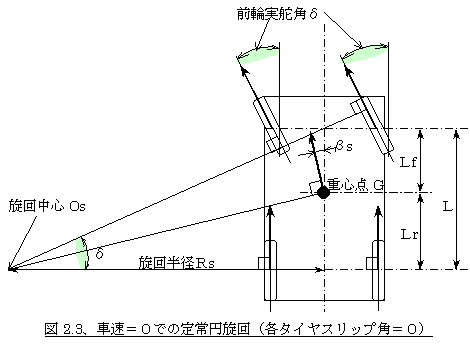
�}�ŁA�f�F�ԗ��d�S�_�A�F�O�֑NJp�A�k�F�z�C�[���x�[�X�A�k���F�O���`�d�S�_�����A�k���F�㎲�`�d�S�_�����A�q���F���a�A�n���F���S�A��s�F�d�S�_�̎ԑ̃X���b�v�p�ł��B
�@���̏�Ԃł͎ԑ����Ȃ����߉��S�́i���S�́j�͓����Ă��Ȃ��̂ŁA�O�ցE��ւƂ��Ƀ^�C���ɃX���b�v�p�͕t���Ă��܂���B�]���đO�ֈʒu�ł͑O�ւ��̂��̂̕����A��ֈʒu�ł͌�ւ��̂��̂̕����ɐi�����Ƃ��Ă���ƍl���邱�Ƃ��ł��܂��B�]���Ă��̐��S�͑O��ւ̌����ɒ��p�Ȑ��̌�_�n���ɂȂ�܂��B����炩���}��A
�@�q���~���������k
�����Ń������ł���i�k�͂q���ɑ��ď\���������j�Ƃ���ƁA
�@���������@�@�@����@�@�@�q�����k�^�@�@�@�@�@�@�c�i�Q�|�P�j
�ƂȂ�܂��B���A���S�n���Əd�S�_�������ɒ��p�ȃx�N�g�����d�S�_�̐i�s�����ŁA���̍�}������i�d�S�_�́j�ԑ̃X���b�v�p��s���ŏ��A�i�s�����ɑ��Ďԗ����O�������Ă����Ԃł��邱�Ƃ��킩��܂��B�܂����̑傫���́A
�������������������k���^�q��
�ƂȂ�܂��B
�@�����}2.4�͐���̎ԗ��������O�֑NJp�ŁA���鑬�x�������Đ��Ă����Ԃ�\���Ă��܂��B
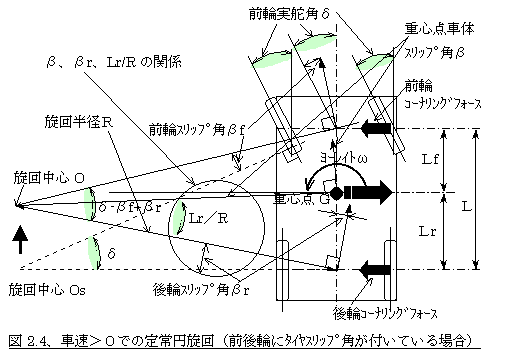
�}�ŁA�f�F�ԗ��d�S�_�A���F�d�S�_�ԑ̽د�ߊp�A�F�O�֑NJp�A�����F�O�փ^�C���X���b�v�p�A�����F��փ^�C���X���b�v�p�A�ցF���[���C�g�i����p���x�j�A�k�F�z�C�[���x�[�X�A�k���F�O���`�d�S�_�����A�k���F�㎲�`�d�S�_�����A�q�F���a�A�n�F���S�A�ł��B
�@���̏�Ԃł͎ԑ������邽�ߏd�S�_�ɉ��S�́i���S�́j�������Ă���A����ɑΉ����ă^�C���̓R�[�i�����O�t�H�[�X�����Ă��Ȃ���Ȃ�܂���B�]���đO��ւɃ^�C���X���b�v�p�����Ă��܂��B�܂�����ɔ����A�ԗ��ɂ͂��̎ԑ��Ɛ��a�ɑΉ����郈�[���C�g�ցi����p���x�j���������Ă��܂��B
���đO��ւɃ^�C���X���b�v�p���t���Ă���̂ŁA�O�ֈʒu�A��ֈʒu�̐i�s�����̓^�C���̌������炻�ꂼ������A�������ꂽ�����ƂȂ�܂��B�����Đ��S�͂��ꂼ��̐i�s�����ɒ��p�Ȑ��̌�_�n�ƂȂ�̂ŁA���a�q�͍�}��
�@�q�~�������i�|�����{�����j���k
�����Łi�|�����{�����j�������Ȃ�A
�������i�|�����{�����j���i�|�����{�����j
�����
�@�q�~�i�|�����{�����j���k
�@�q���k�^�i�|�����{�����j�@�@�@�@�@�@�@�@�@�@�c�i�Q�|�Q�j
�ƂȂ�܂��B
�܂��A�ԑ����O�̂Ƃ��̐��SO���ɑ��āA�ԑ����O�̂Ƃ��̐��SO�́A����������̕������ԑ̂��猩�đO���Ɉړ����A���̗ʂ͐�������x�������قǁi�����A�������傫���قǁj�����邱�Ƃ��킩��܂��B
���A�}2.4�̉~���̃��A�����A�k���^�q�̊W����A�ԑ̃X���b�v�p���́A
�@�����k���^�q�|����
 �ƂȂ邱�Ƃ��킩��܂��B�܂���͍ŏ��������k���^�q���i�ԑ̂��O�����j�ŁA�������傫���Ȃ�ɂ�i��������x���オ��ɂ�j�O�����̊p�x�������Ă����A�₪�ĂO�ƂȂ�A����ɂ͓������ɂȂ�ƌ������Ƃł��B�����Ŏԗ������a���̒��~��������Ă���A�܂�q�����ł���A���́i�O�����p�x�́j�����ʂ̓����Ɉ�v���܂��B������O���t�ŕ\���A�}2.5�̂悤�ɂȂ�܂��B
�ƂȂ邱�Ƃ��킩��܂��B�܂���͍ŏ��������k���^�q���i�ԑ̂��O�����j�ŁA�������傫���Ȃ�ɂ�i��������x���オ��ɂ�j�O�����̊p�x�������Ă����A�₪�ĂO�ƂȂ�A����ɂ͓������ɂȂ�ƌ������Ƃł��B�����Ŏԗ������a���̒��~��������Ă���A�܂�q�����ł���A���́i�O�����p�x�́j�����ʂ̓����Ɉ�v���܂��B������O���t�ŕ\���A�}2.5�̂悤�ɂȂ�܂��B
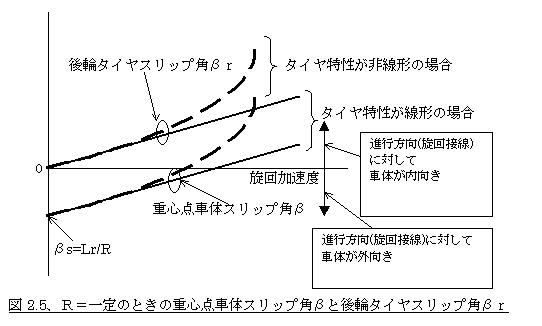
���Ă����Łi�Q�|�Q�j�̎�������A�܂���}�ォ����킩��悤�ɁA�����O�փ^�C���X���b�v�p�����ƌ�փ^�C���X���b�v�p��������������A
�@�����|�������O�@�@�@�ƂȂ�A�����
�@�q���k�^�@�@�@�ƂȂ��āA���Ȃ킿���i�Q�|�P�j���
�@�q���q���@�@�@�ƂȂ�A
����͎ԑ����オ���Ă����a���ς��Ȃ��u�j���[�g�����X�e�A�v�����ł���Ƃ������Ƃ��킩��܂��B
���l�ɂ���
�@�����|�������O�@�@�@�Ȃ�A���i�Q�|�Q�j�̕���ł���i�|�����{�����j��
�@�i�|�����{�����j���@�@�@�ƂȂ�
�@�q���q���@�@�@�ƂȂ���
�ԑ����オ��Ɛ��a���傫���Ȃ�A���Ȃ킿�u�A���_�[�X�e�A�v�����ł��邱�Ƃ��킩��܂��B
���l��
�@�����|�������O�@�@�@�Ȃ�A�q�̕���ł���i�|�����{�����j��
�@�i�|�����{�����j���@�@�@�ƂȂ�
�@�q���q��
���Ȃ킿�u�I�[�o�[�X�e�A�v�����Ƃ����킯�ł��B
�@�܂Ƃ߂�ƁA�������Ԃɂ����đO�ւ̃^�C���X���b�v�p����ւ����傫���ꍇ�́u�A���_�[�X�e�A�v�ł���A�������ꍇ�́u�j���[�g�����X�e�A�v�A�������ꍇ�́u�I�[�o�[�X�e�A�v�ł���Ƃ������Ƃł��B
�����̍��ڂց��@�@���ڎ��ց��@�@���g�n�l�d�ց�