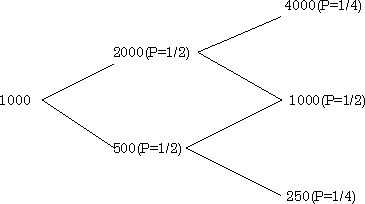
| 3− オプションのゲーム化 株式については元ゲーム、オプションについては派生ゲームと完全にゲーム化して考える。 下記で、コインによる上下変動(上昇か下落かの二つの状態)を考えるのが2項モデルである。 コインを2回振るのが2期モデルである。例えば、サイコロによる6種類の変動を考えるのではうまくいかない。(2項モデルのみ有功) それに反して、コインは何回振っても同じ議論ができる。N回振ると、N期モデルになる。 元ゲーム AとBが次のようなゲームをする。(元ゲームと名づける。) 最初の額を1000円とし、AはBに払う。コインを振り、表がでたら金額は2倍、裏がでたら、1/2倍となるものとする。 コインを2回振って、BはAに「確定した金額」を払う。(以下Pは確率) |
|
Aから見た期待値は、約1562円となり、1000円より大きいから、Aに有利なゲームであるが、裁定機会はない。 派生ゲーム AとBが以下のようなゲームをする。(派生ゲームと名づける。) 設定は、元ゲームとほぼ同じであるが、Aは最初に1000円をBに払わず、勝負が決まった時点で、予め約束していた金額(例えば800円)を払う。 しかも、Aは自分が損と分かれば、このゲームへの不参加を決めることも出来る。(ゲームはなかったことにする。) すると、以下のようになる。 4000円になったとすれば、800円を払うから、差し引き3200円の儲けとなる。 1000円になったとすれば、差し引き200円の儲けとなる。 250円になったとすれば、不参加だから、0円の儲けとなる。 Bに勝つ機会は全くないから、このゲームは裁定機会有りとなる。 まともなゲームにするためには、どうすべきか? AはBに、「ゲームへの参加、不参加を決める権利の代金」を予め払えばよい。 Bは代金を受け取ったのだから、Aに従わなければならない。 この代金をいくらにすべきか? 3200円以上なら、Aが儲かる可能性は全くないから、これより小さくすれば、まともなゲーム(無裁定のゲーム)となる。 もっときちんとした価格を決められないだろうか? Aから見た場合、以下のようになる。 3200円儲かる確率 1/4 200円儲かる確率 1/2 0円儲かる確率 1/4 期待値は、900円であるから、AからBに払う権利の代金も900円とすれば公平となる。 ところが、これは、派生ゲームしかない(元ゲームはない)とした場合の公平さである。(派生ゲームだけでも、ゲームは成立する) 驚くべきことに、このような決め方では、元ゲームも考えて派生ゲームとうまく組み合わせると、裁定機会が生じてしまうのだ。 裁定機会が生じない価格は、唯一である。このケースの場合は、金利を考えないと445円となる。(金利については後述) これが、ブラック・ショールズの着想である。 |