<8−3、コンプライアンスステア及びステアリング剛性の概念とその影響>
車両が旋回しているときサスペンションにはどのような変化があるでしょうか。ひとつはストローク変化で、基本的には旋回加速度に比例して車体ロール角が増えていくため、ロール(ストローク)に対するトー角変化がステア特性に影響することを前項で説明しました。もう一つ、車両が旋回するとき、タイヤに横力が発生するためサスペンションにこの力が入力されます。そしてこの力も基本的には旋回加速度に比例して増えていきます。旋回に伴いタイヤからサスペンションに入力される力の大きさは半端ではありません。例えば重さ1600kgの車両が0.5G旋回(少しきつめの旋回)をしているとき、単純計算で1輪あたり1600×0.5/4=200kgf(前外輪ではさらにずっと大きい)の横力が入力されているわけです。コンプライアンスステアとはこのような力の入力によってリンク取り付け点のブッシュなど各部がたわむことによるトー角変化のことで、ロールステアと同様にステア特性に影響します。
なぜ力が入力されるとトー角変化を起こすのでしょうか。サスペンションはその使命から各リンクの取付点にゴムのブッシュ等を介しています。そうでないと振動が吸収できず、とても乗っていられない乗心地となるだけでなく、サスペンション自体がいずれ壊れてしまうからです。また、一部のサスペンションには、このブッシュ部分の変形による逃げがないと、厳密には幾何学的にストロークできないものもあります。しかしゴムを介して取り付けられているということは、力が入ったときにその部分が変形してサスペンションの配置が変化するということになります。これによって引き起こされるトー角変化をコンプライアンスステアといい、横力によるものだけでなく、制動や駆動による前後力などに対して起こります。ここでは旋回を考える上で代表的な横力によるコンプライアンスステアの簡単な例について説明しましょう。
いま図8.4のようなリンク配置のサスペンションがあったとします。このサスペンションに図のように内引き方向のタイヤ横力が入力されたとします。ところでこの図でタイヤ横力がタイヤ接地点中心より若干後ろに書かれていますが、この距離のことをニューマッチックトレールということは、<7−4、ニューマチックトレールとセルフアライニングトルクについて>のところで説明しました。
![]()
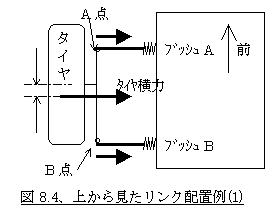
このタイヤ横力の着力点が今たまたま前後2つのリンクのちょうど中央だったとします。すなわち、それぞれのリンクに入力される力は同じなので、もしブッシュAとブッシュBの剛性が同じであれば、両者は同じだけたわみ、その結果A点もB点も同じだけ内側にはいることになります。したがってこの例では、この横力によるトー角変化はゼロということになります。
しかしもしブッシュAの剛性がブッシュBより低かったらどうなるでしょうか。その場合はブッシュAの方がより多くたわみ、結果としてA点がB点より内側にはいることになります。すなわち内引きの横力によりトーイン方向にトー角変化するわけです。
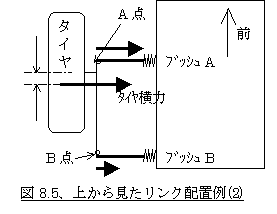
さらに図8.5のように横力の着力点が例えば前側によったリンク配置だったらどうなるでしょうか。この場合、ブッシュAとブッシュBの剛性が同じでも、前側のリンクと後ろ側のリンクが分担する横力は「横力の着力点〜各リンク間距離」の逆比となり前側のリンクへの入力の方が大きいため、ブッシュAがより多くたわみ、A点がより内側に変位してトーインとなります。もしブッシュAの剛性がブッシュBより低ければ、この傾向はさらに強くなります。
![]()
以上が横力によるコンプライアンスステアの基本的な発生概念ですが、横力によるコンプライアンスステアがステア特性に与える影響の方向性については、前輪であれば内引き力(外輪相当)でトーアウトのもの(すなわち外引き力でトーインのもの)がUS(アンダーステア)、後輪なら内引き力でトーイン(すなわち外引き力でトーアウト)のものがUSのコンプライアンスになります。
例えばここに元々はニュートラルステアの車両があったとして、その後輪のサスペンションを仮に内引き力100kgfに対して0.2°トーイン(外引きに対してはトーアウト)に切れるコンプライアンスステアのものと換えたらどうなるか。この車両が車重2000kg、重量配分50:50だとすると、後軸重は1000kgですから、0.2G旋回で後輪の左右輪にはそれぞれ100kgfの横力が入力されるわけです(内外輪横力差等無視して)。そうするとコンプライアンスにより、後内外輪はそれぞれ旋回内側へ0.2°切れることになります。0.4Gなら0.4°です。するとこの車両は<8−1、ロールステアの概念とその影響>の項と同じ説明で、同じアンダーステアの特性を有することになることがわかると思います。
ところで前輪においては操舵のためのステアリング装置が付いていてその剛性がトー角変化に影響しますが、このステアリング剛性によるトー角変化と横力によるコンプライアンスステアの関係について書いておきます。例えば図8.6左のように、前側にAの字型のアームが上下にあってその間にキングピンが設定され、そして後ろ側にこの回転軸回りのモーメントを支えるようにステアリングギアのタイロッドが1本あるようなサスペンションレイアウトを考えます。キングピンというのは<7−4、ニューマチックトレールとセルフアライニングトルクについて>の項で説明したように、転舵方向の回転軸のことです。
![]()
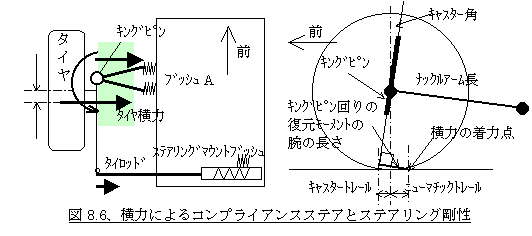
さて今タイヤに内引きの横力が発生したとしてこの横力をどのリンクがどのくらい受け持つか考えてみましょう。このサスペンションを横から見ると図8.6右のようにキングピンが傾きを持っています。これがキャスター角でその延長線と地面の交わる点とタイヤ接地点との距離をキャスタートレールということは、同じく<7−4、ニューマチックトレールとセルフアライニングトルクについて>の項で述べました。タイヤ横力はさらにニューマチックトレール分後ろに入力されるわけですから、前側のリンクと後ろ側のリンクが分担する横力は、前述の考え方に従ってそれぞれ「キャスタートレール+ニューマチックトレール」と「横力着力点〜後方リンク間距離」の逆比となります。つまり前者を=a、後者を=b、横力を=Yとすると、
前方のリンク(上下トータルで)には{b/(a+b)}×Y、
後方のリンクには{a/(a+b)}×Y
が入力されます。(前方のリンクは上下2本なので本当は更に高さの逆比でそれぞれに分割されますが、ここでは省略します)
これまでの例と同じように考え、前側のリンクに入力される{b/(a+b)}×YによりトータルとしてのブッシュAがたわむ量と、後ろ側のリンクに入力される{a/(a+b)}×Yによりステアリングマウントブッシュ等がたわむ量のバランスでトー角変化が起きるコンプライアンスステアととらえることができるわけですが、一方で後ろのリンクへの入力、すなわちステアリング系への入力に着目すると、
前後のリンク間スパンをLとして、
b=L−aだから、後方のリンク、タイロッドへの入力は、
{a/(a+L−a)}×Y=(a/L)×Y …(8−1)
となります。つまりタイロッドは、キングピン回りに発生するa×Yすなわち「(キャスタートレール+ニューマチックトレール)×横力」のモーメントを、Lすなわち「前後のリンク間スパン」、つまり「キングピン〜後方のリンク間スパン(ナックルアーム長)」で受け持っているということになります。そしてこのモーメントによる圧縮力(内輪は引張力)を受けるのはステアリングギアのマウントブッシュをはじめとするステアリング剛性ということになります。したがってこのモーメントによるステア分をステアリング剛性分のトー変化ととらえることがあります。式(8−1)からこのトー変化分は、同じ横力に対してキャスタートレール+ニューマチックトレールが大きいほど、ステアリングギア剛性が低いほど、キングピン〜タイロッド間スパンが短いほど、大きくなることがわかります。