＜７−１、タイヤ変形のモデルによる横力の説明＞
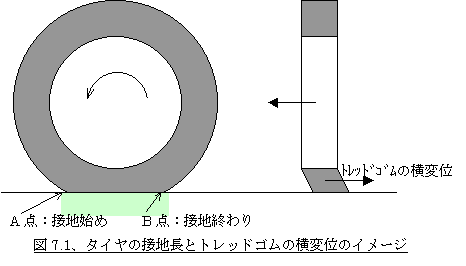
最初にタイヤが路面に接地している状況を考えてください。タイヤは中空のゴムでできているので荷重によりたわんで、ある接地長を持っています。つまり転がっていきながらある点で接地し始め、ある点で接地し終わるその長さのことです（図7.1左参照）。また、タイヤを横方向に滑らせると、つまりタイヤにスリップ角が付くと、剛体であるホイールに対してタイヤのトレッドゴムは横方向に変位します（図7.1右参照）。但しこの横変位量は接地長全体で一様ではありません。
いま、タイヤにスリップ角αが付いているものとします。つまりタイヤは全体としてはタイヤの向きに対してαの向きに転動して（転がって）いるわけです。このときタイヤのトレッド面は接地している範囲でどのような横変位をしているのでしょうか。
図7.2はスリップ角の付いているタイヤの接地面を上から見た図です。タイヤ（ホイール）の中心線ｘ軸が元々のタイヤの向き（ホイールの向き）でタイヤの進行方向はこれに対してαだけ斜めの線になります。
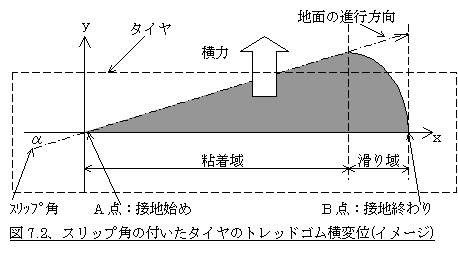
タイヤはＡ点で接地し始めますが、このポイントではタイヤのトレッドは直前まで路面と接触していないので無理なく接地しています。しかしこれ以降はタイヤの進行方向（言い換えればタイヤから見れば路面の進行方向）はαだけずれていますからトレッド面は路面に引きずられてタイヤの中心線からαのラインに沿ってずれてたわんでいきます。トレッドゴムが横方向にたわむことでこのずれに合わせ路面との密着を保っているわけです。このように路面と密着してスリップ角分だけたわんでいる部分のことを粘着域といいます。ところで接地終わりのポイントＢ点を考えてみると、このポイントではタイヤが路面から離れて、路面から引きずられていないわけですから、トレッドはタイヤ中心線に戻らなければなりません。従ってαに沿ってたわんできたトレッド面はＢ点近くで急速につじつまを合わせるため横方向の変形を戻さなければなりません。すなわちこの部分ではトレッド面は路面についていけず路面とトレッド面が滑っている状態です。この部分のことを滑り域といいます。そしてこの粘着域と滑り域のたわみ量を接地長全体で合計し（積分し）、トレッドゴムの横剛性をかけた値（すなわち学校で習ったＦ（力）＝ｋ（バネ定数＝横剛性）×Ｘ（変位＝たわみ量）がタイヤに発生する横力というわけです。そしてもちろん前に説明したようにコーナリングフォースはその定義から、横力のスリップ角αのラインに直角な成分（横力×ｃｏｓα）ということになります。スポーティーなタイヤは一般的にトレッド剛性が高い理由がこのことからも理解できると思います。トレッド剛性が高いと同じスリップ角がついて同じだけたわんでもそれにかけるところのバネ定数が高いわけですから発生する横力は大きいというわけです。
ところでスポーティーなタイヤというのは「ハイグリップな」というイメージもあるかと思いますが、このハイグリップすなわち摩擦係数μの高さはどこででてくるのか。これは前述の粘着域と滑り域の境界に関係しています。トレッド面はどこまで路面と密着し、どこから滑り始めるのか。それは「トレッド剛性×トレッドの横変位量」が「タイヤと路面の摩擦係数μ×（単位接地長あたりの）荷重」となるポイントから先で滑り始めるということです。荷重（すなわち垂直抗力）にμをかけた摩擦力でトレッド面を横に引っ張っているわけですからどんどん引っ張って横変位が大きくなり「剛性×変位」に摩擦力が負けたとき滑り始めるというわけです。
もしここでトレッド剛性が同一でμが異なる２つのタイヤがあったとして、これに同じ輪荷重、同じ（比較的大きな）スリップ角を与えたらどうなるか考えてみましょう。μが低い方が早く変位の限界に達するため粘着域のピークの変位が小さくなります。それにより図7.3のように粘着域と滑り域で形作られる三角形に似た変位の面積が山の高さが小さくなるわけです。
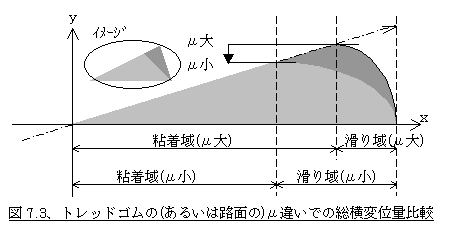
従ってμの低いタイヤの方が同じ条件での横力（コーナリングフォース）が小さくなるということになります。つまり同一条件でコーナリングフォースを多く発生するタイヤとは、トレッドの横剛性は高く、トレッド面のμは高くということになるわけです。尚、摩擦係数は相手があってのものですから、同じタイヤで路面μが違う場合もまったく同じことで、路面μが低い方が（特にスリップ角の大きい領域で）コーナリングフォースは小さくなります。これはウェット路面や雪道などで皆さん経験済みですね。