���S�|�Q�A���E�d�ړ��ɂ����郍�[���Z���^�[���ƃ��[�������O��z����
�@�Ƃ���őO�q�̃��[�������O��z���ɂ�鍶�E�d�ړ��O��z���̃R���g���[���ɂ��Ă̐����́A�ȗ��̂��ߏd�v�ȗv�f���P�Ȃ��Ă��܂��B�����ɂ͂P�����ł͂Ȃ��̂ł����A���[�������O��z���ƃZ�b�g�ōl����ׂ��d�v�ȗv�f�Ƃ����Ӗ��ŁA������₱�����Ă��u���[���Z���^�[���v�͂�͂�������Ă����ׂ����Ǝv���܂��B
�@�Ԃ��t�����g�i�܂��̓��A�j���猩�Ă݂Ă��������B�Ԃ����[������Ƃ����Ă��ǂ��i�ǂ̍����j�𒆐S�Ƀ��[������̂��Ƃ����^�₪�����邱�ƂƎv���܂��B���̍��������[���Z���^�[���ł���A�O�セ�ꂼ��ɃT�X�y���V�����W�I���g���ɂ���Č��܂郍�[���Z���^�[�������݂��܂��B���Ȃ킿�Ԃ̓t�����g�ƃ��A�̃��[���Z���^�[���������̉������[������킯�ł��B
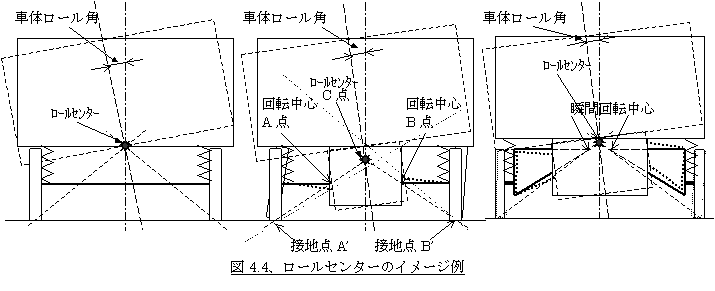
�t�����g�������̓��A�T�X�y���V�����̃��[���Z���^�[���̓t�����g�i�܂��̓��A�j���猩���Ƃ��̍��E�̃T�X�y���V�����̏u�ԉ�]���S�i���T�|�Q�A�T�X�y���V�����̏u�ԉ�]���S�ɂ��ā��Q�Ɓj�ƃ^�C���ڒn�_�������̍��E�̌�_�ɂȂ�܂��i�}4.4�Q�Ɓj�B�}4.4�̒����̐}���ɐ�������ƁA�����č��̐ڒn�_A�f��A�𒆐S�ɓ����̂ŁA�����X�g���[�N�ł�A�f�\A�ɐ����ɓ������ƂɂȂ肻�̏u�Ԓ��S��A�f�\A�̉�����ɂ�����̂ƍl�����܂��BB�f�����l��B�f�\B�̉�����ɂ���ƍl������̂ŁA���E�̃^�C���ڒn�_�̉�]���S�A���Ȃ킿���[���Z���^�[�͂��̗�������������|�C���g�ł����_C�ƂȂ�܂��B�A���Ɨ����˃T�X�y���V�����Ȃǂ̏ꍇ�A����͂��̈ʒu�ł̔����X�g���[�N�Ő��藧�b�ŁA�T�X�y���V�������傫���X�g���[�N���Ă����Ǝԑ̂��猩�ă^�C���ڒn�_�̈ʒu���ω����Ă������߁A���̓��[���Z���^�[�����ω����Ă����܂��B�ԍ����ς����[���Z���^�[�����ς��܂����A���[���i�Зւ̓o�E���h�ŕЗւ̓��o�E���h�j���Ă������E�̒��S�ɂ���Ƃ�����܂���B�}4.4�����̗�ł����[���������Ƃ̃C���[�W�ł���_���Őڒn�_�ƃT�X�y���V�����̉�]���S�������̌�_�͂��͂�ŏ��̌�_�ƈ�v���Ȃ��킯�ł��B�T�X�y���V�����`���ɂ���Ă͍��E�̃T�X�y���V�����̏u�ԉ�]���S���̂��X�g���[�N�ʒu�ɂ���đQ���ω����Ă����܂��B�܂肱�̊T�O�͌����Ɍ����ƁA����ʒu�i�Ⴆ�Ί�p���̐����ʒu�j����̔����X�g���[�N�Ɍ��肵���b�Ƃ������ƂɂȂ�܂��B
�����������ł͂����������G�Șb�͒u���Ă����āA�O��̃T�X�y���V�����ɂ��ꂼ�ꂠ��Œ肵�����[���Z���^�[�������݂��A�Ԃ͑O��̃��[���Z���^�[�����������Ƀ��[������Ɠ��ɂ����Ă��������B���̍����������ł͂��ꂼ��g���i�O�j�A�g���i��j�Ƃ��܂��B�܂��d�S�����g���Ƃ��A�d�S�ʒu�i�O������j�ł̃��[���Z���^�[���̍������g���Ƃ��܂��B�O��̃g���b�h���s���A�s���Ƃ��A�ԏd���v�A�O���d���v���A�㎲�d���v���A�t�����g�̃��[���������f���A���A���f���A���݂̒��~����ɂ�����ԑ̃��[���p���ӁA��������x���x���B�����đO��ւ̍��E�d�ړ��ʂ����ꂼ�ꃢ�v���A���v���Ƃ��܂��i�}4.5�Q�Ɓj�B
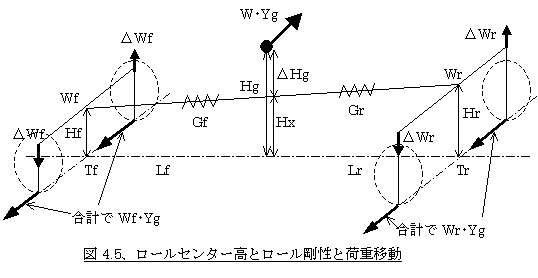
�����łg���|�g�������g���Ƃ���ƁA�d�S�ɐ�������x�������邱�Ƃɂ�郍�[���Z���^�[�����̃��[�����g�͂v�~�x���~���g���ƂȂ�A���̃��[�����g��O��̃��[�������Ŏ~�߂�킯�ł�����A
�v�E�x���E���g�����i�v���{�v���j�E�x���E���g�����i�f���{�f���j�E�Ӂ@�@�c�i�S�|�P�j
�ƂȂ�܂��B�X�Ƀt�����g�̃��[���Z���^�[���̃��[�����g�̒ނ荇������A
�f���E�Ӂ����v���E�s���|�v���E�x���E�g���@�@�c�i�S�|�Q�j
�����łv���E�x���͑O�ցi���E�֍��v�j�ɂ�����R�[�i�����O�t�H�[�X�̒l�ŁA���ݒ��~���Ƃ����O��Ȃ̂őO��ւɓ����R�[�i�����O�t�H�[�X�͑O���d�A�㎲�d���ꂼ��ɐ�������x�����������̂ƂȂ�i�������Ȃ��Əd�S�_����̑O��̃R�[�i�����O�t�H�[�X���ނ荇��Ȃ��̂Œ��~���Ȃ��B���P�|�Q�A�n���h�����ƂȂ��Ԃ̓R�[�i�����O����H���̍��Q�Ɓj���Ƃ��狁�߂��܂��B���l�Ƀ��A�̃��[���Z���^�[���̃��[�����g�̒ނ荇������A
�@�f���E�Ӂ����v���E�s���|�v���E�x���E�g���@�@�c�i�S�|�R�j
���i�S�|�P�j���
�Ӂ��i�v���{�v���j�E�x���E���g���^�i�f���{�f���j�@�@�c�i�S�|�S�j
���i�S�|�S�j�����i�S�|�Q�j�֑��
�@�f���E�i�v���{�v���j�E�x���E���g���^�i�f���{�f���j�����v���E�s���|�v���E�x���E�g��
�����
�@�@�@�@�@�o�f���^�i�f���{�f���j�p�E�i�v���{�v���j�E���g���{�v���E�g��
���v�����\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�E�x��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�c�i�S�|�T�j
���i�S�|�S�j�����i�S�|�R�j�֑��
�@�f���E�i�v���{�v���j�E�x���E���g���^�i�f���{�f���j�����v���E�s���|�v���E�x���E�g��
�����
�@�@�@�@�@�o�f���^�i�f���{�f���j�p�E�i�v���{�v���j�E���g���{�v���E�g��
���v�����\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�E�x��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�c�i�S�|�U�j
�����Ŏ��i�S�|�T�j�Ǝ��i�S�|�U�j�ɂ��āA�@�Ԏ��@�͂��ꂼ�ꃍ�[�������̑O��z���̂��Ƃł���i�v���{�v���j�͂������ԏd�v�A�O��̃g���b�h�s���Ƃs���͕��ʂ͂��܂�ς��Ȃ��̂œ����Ƃ���ƁA
�@���v�����i���[�������t�����g�z���~�v�~���g���@�{�@�v���~�g���j�~��������x�^�g���b�h
�@���v�����i���[���������A�z���~�v�~���g���@�{�@�v���~�g���j�~��������x�^�g���b�h
�ƂȂ�܂��B���̂Q�̎��������l���Ă݂�ƁA�����O��̃��[���Z���^�[���g�����g���i���g���j���O�Ȃ�A
�@���v�����i���[�������t�����g�z���~�v�~�g���j�~��������x�^�g���b�h
�@���v�����i���[���������A�z���~�v�~�g���j�~��������x�^�g���b�h
�ƂȂ�A�ŏ��̐����̂悤�Ƀ��v���ƃ��v���̓��[�������O��z���ɏ]�����ƂɂȂ�܂��B�c�@�@�@
�܂��A�����O�E��̃��[���Z���^�[�����d�S���Ɠ��������A���Ȃ킿�g�����g�����g��
����ă��g�����O�Ȃ�A
�@���v�����v���~�g���~��������x�^�g���b�h
�@���v�����v���~�g���~��������x�^�g���b�h
�ƂȂ�A�v���A�v���A���Ȃ킿�����̑O��d�ʔz���ɏ]���č��E�d�ړ����邱�Ƃ��킩��܂��B�@�@�@�c�@�@�A
�A���A���̏ꍇ���[�������Ɂi�d�S�_�ɂ�����j��������x�ɂ�郂�[�����g���������Ȃ����߁i�O��̃��[���Z���^�[���Əd�S������������������j�A���[���p�̓[���i�^�C���̂���ݕ��͏����j�Ƃ������ƂɂȂ�܂��B
�X�Ƀ��g�����O�i�g�����g���j�ł͂��邪�A�g���Ƃg�����A���o�����X�ȏꍇ��
�@���v�����v���~�g���~��������x�^�g���b�h
�@���v�����v���~�g���~��������x�^�g���b�h
�ƂȂ�A�O��ւ̍��E�d�ړ��ʂ͂v���~�g���A�v���~�g���A���Ȃ킿�O��́A�����d�ƃ��[���Z���^�[���̐ςɏ]�����ƂɂȂ�܂��B�@�@�@�c�@�@�B
�ł͂����ŁA���ۂɐ��������Ă������̗�ɂ��Čv�Z���Ă݂܂��傤�B�������Ȃ�ׂ��P���ɂ��邽�߁A��Ƃ��Ďԗ��d�ʂv���P�O�O�O�������A�O��d�ʔz�����O�D�T�i�v�����v�����T�O�O�������j�A�g���b�h�s�����s�����P�D�Q�T���A�d�S���g�����O�D�T���A�O��g�[�^�����[�������i�f���{�f���j���T�O�O�O�������E���^�������A���[�������O��z�����O�D�T�i�f�����f�����Q�T�O�O�������E���^�������j�A���[���Z���^�[���g���A�g�����O�D�Q�T���̎ԗ�������f���O�D�T�f�Œ��~���Ă�������ɁA�O��d�ʔz�����O�D�U�`�O�D�S�A���[�������O��z�����O�D�U�`�O�D�S�A�O�ネ�[���Z���^�[�����O�`�O�D�W�ɐU���Ă݂Ă��ꂼ�ꍶ�E�d�ړ��ʂ��O��ւłǂ��Ȃ邩�݂Ă݂܂��B
�ŏ��ɑO��g�[�^���̍��E�d�ړ��ʂ�
���E�d�ړ��ʁ��ԗ��d�ʁ~����G�~�d�S���^�g���b�h
���P�O�O�O�~�O�D�T�~�O�D�T�^�P�D�Q�T
���Q�O�O�������i�O��g�[�^���j
���Ƀ��[���p�i�Q�l�j���v�Z���Ă����܂��傤�B���i�S�|�P�j����
�v�E�x���E���g�����i�f���{�f���j�E��
�����
�Ӂ��v�E�x���E���g���^�i�f���{�f���j
����A�g�����g�����O�D�Q�T�̏ꍇ�A���g�����O�D�T�|�O�D�Q�T���O�D�Q�T��������
�@�Ӂ��P�O�O�O�~�O�D�T�~�O�D�Q�T�^�T�O�O�O���O�D�O�Q�T���������P�D�S�R������
�܂��A�g�����g�����O�̏ꍇ�A���g�����O�D�T�|�O���O�D�T����
�@�Ӂ��P�O�O�O�~�O�D�T�~�O�D�T�^�T�O�O�O���O�D�O�T���������Q�D�W�U������
�܂��A�g�����g�����O�D�T�̏ꍇ�A���g�����O�D�T�|�O�D�T���O����
�@�Ӂ��P�O�O�O�~�O�D�T�~�O�^�T�O�O�O���O������
�܂��A�g�����g�����O�D�P�̏ꍇ�A���g�����O�D�T�|�O�D�P���O�D�S����
�@�Ӂ��P�O�O�O�~�O�D�T�~�O�D�S�^�T�O�O�O���O�D�O�S���������Q�D�Q�X������
�����đO��ւ��ꂼ��̍��E�d�ړ��ʂ͎��i�S�|�T�j�i�S�|�U�j����
�@���v�����i�u���[�������t�����g�z���v�~�ԗ��d�ʂv�~���g���{�v���~�g���j�~�x���^�s��
�@���v�����i�u���[���������A�z���v�~�ԗ��d�ʂv�~���g���{�v���~�g���j�~�x���^�s��
����Ċ�̏ꍇ��
�@���v�����i�O�D�T�~�P�O�O�O�~�O�D�Q�T�{�T�O�O�~�O�D�Q�T�j�~�O�D�T�^�P�D�Q�T
�@�@�@�@���P�O�O������
�@���v�����i�O�D�T�~�P�O�O�O�~�O�D�Q�T�{�T�O�O�~�O�D�Q�T�j�~�O�D�T�^�P�D�Q�T
�@�@�@�@���P�O�O������
�ƂȂ�A���E�d�ړ��̑O��z���͂T�O�F�T�O�ƂȂ�܂��B���Ȃ݂ɑO��̃��[�������z����O��d�ʁA�O��̃��[���Z���^�[�����ǂ̂悤�Ȓl�ɂ��Ă��A���ꂼ��̑O��䂪�T�O�F�T�O�Ȃ�A���E�d�ړ��̑O��z���͏�ɂT�O�F�T�O�ƂȂ�܂��B
����ɑ��Ă��ꂼ��̗v�f�̒l��U�����ꍇ�̌v�Z���ʂ��\4.1�`4.3�ł��B
�\4.1�A��ɑ����[�������O��z���ƑO��d�ʔz����U�����ꍇ�̍��E�d�ړ�
|
�f�� |
�f�� |
�v�� |
�v�� |
�g�� |
�g�� |
���g�� |
��deg |
���v�� |
���v�� |
|
2500 |
2500 |
500 |
500 |
0.25 |
0.25 |
0.25 |
1.43 |
100 |
100 |
|
3000 |
2000 |
�� |
�� |
�� |
�� |
�� |
�� |
110 |
90 |
|
2000 |
3000 |
�� |
�� |
�� |
�� |
�� |
�� |
90 |
110 |
|
2500 |
2500 |
600 |
400 |
�� |
�� |
�� |
�� |
110 |
90 |
|
�� |
�� |
400 |
600 |
�� |
�� |
�� |
�� |
90 |
110 |
|
2500 |
2500 |
500 |
500 |
0.1 |
0.1 |
0.4 |
2.29 |
100 |
100 |
|
3000 |
2000 |
�� |
�� |
�� |
�� |
�� |
�� |
116 |
84 |
|
2000 |
3000 |
�� |
�� |
�� |
�� |
�� |
�� |
84 |
116 |
|
2500 |
2500 |
600 |
400 |
�� |
�� |
�� |
�� |
104 |
96 |
|
�� |
�� |
400 |
600 |
�� |
�� |
�� |
�� |
96 |
104 |
�\4.2�AHf=Hr=0�y��=0.5����Ƀ��[�������z���Əd�ʔz���U�����ꍇ�̍��E�d�ړ�
|
�f�� |
�f�� |
�v�� |
�v�� |
�g�� |
�g�� |
���g�� |
��deg |
���v�� |
���v�� |
|
2500 |
2500 |
500 |
500 |
0 |
0 |
0.5 |
2.86 |
100 |
100 |
|
3000 |
2000 |
�� |
�� |
�� |
�� |
�� |
�� |
120 |
80 |
|
2000 |
3000 |
�� |
�� |
�� |
�� |
�� |
�� |
80 |
120 |
|
2500 |
2500 |
600 |
400 |
�� |
�� |
�� |
�� |
100 |
100 |
|
�� |
�� |
400 |
600 |
�� |
�� |
�� |
�� |
100 |
100 |
|
2500 |
2500 |
500 |
500 |
0.5 |
0.5 |
0 |
0 |
100 |
100 |
|
3000 |
2000 |
�� |
�� |
�� |
�� |
�� |
�� |
100 |
100 |
|
2000 |
3000 |
�� |
�� |
�� |
�� |
�� |
�� |
100 |
100 |
|
2500 |
2500 |
600 |
400 |
�� |
�� |
�� |
�� |
120 |
80 |
|
�� |
�� |
400 |
600 |
�� |
�� |
�� |
�� |
80 |
120 |
�ŏ��ɕ\4.2���݂�ƁA�㔼���̂g�����g�����O�̏ꍇ�ɂ̓��[�������z�������ꂼ��A�U�O�F�S�O�A�S�O�F�U�O�ƐU��ƁA���E�d�ړ��ʂ̑O��z�����U�O�F�S�O�A�S�O�F�U�O�ƂȂ�A�O�q���@�̐����̒ʂ胢�v���ƃ��v���̓��[�������O��z���ɏ]�����Ƃ��킩��܂��B���̏ꍇ�A�d�ʔz����U���Ă����E�d�ړ��ʂɂ͉e������܂���B
�t�ɉ������̂g�����g�����O�D�T�̏ꍇ�ɂ͏d�ʔz�������ꂼ��A�U�O�F�S�O�A�S�O�F�U�O�ƐU��ƁA���E�d�ړ��ʂ̑O��z�����U�O�F�S�O�A�S�O�F�U�O�ƂȂ�A�O�q���A�̐����̒ʂ胢�v���ƃ��v���͏����̑O��d�ʔz���ɏ]�����Ƃ��킩��܂��B���̏ꍇ�A���[�������z����U���Ă����E�d�ړ��ʂɂ͉e������܂���B
���ɕ\4.1�̏㔼�����݂�ƁA��i�g�����g�����O�D�Q�T�j�ɑ��ă��[�������z���Əd�ʔz���̂��ꂼ�������U�O�F�S�O�A�S�O�F�U�O�ƐU��ƁA���E�d�ړ��ʂ̑O��z�����T�T�F�S�T�A�S�T�F�T�T�ƂȂ�܂��B����͂ǂ��䂤���Ƃł��傤���B���̗�ł͊�d�l�̂g�����g�����g���̂��傤�ǂP�^�Q�̂��߁A���E�d�ړ��̑O��z���ɑ���u���[�������z���̉e���v�Ɓu�d�ʔz���̉e���v�͂��ꂼ�ꔼ�����\���Ƃ������Ƃł��B�܂������T�O�F�T�O�Ȃ̂ł��̕��Ńg�[�^���̍��E�d�ړ��ʂQ�O�O�������̔����̂P�O�O���������A�O�T�O�������F��T�O�������ƂȂ�A��������̗v�f���U�O�F�S�O�Ȃ̂Ŏc��̂P�O�O�������ɑ��ĉe�����y�ڂ��ĂU�O�������F�S�O�������ƂȂ�A���v�Łi�T�O�{�U�O�j�������F�i�T�O�{�S�O�j���������T�T�F�S�T�ƂȂ�킯�ł��B
�\4.1�̉������͂g�����g�����O�D�P�ɂ����d�l����ɁA���E�d�ړ��̑O��z���ɑ��郍�[�������z���Əd�ʔz���̉e�����݂����̂ŁA��i�g�����g�����O�D�P�j�ɑ��ă��[�������z���Əd�ʔz�������ꂼ��A�U�O�F�S�O�A�S�O�F�U�O�ƐU��ƁA���E�d�ړ��ʂ̑O��z�������[�������z���̏ꍇ�͂T�W�F�S�Q�A�S�Q�F�T�W�ƂȂ�A�d�ʔz���̏ꍇ�͂T�Q�F�S�W�A�S�W�F�T�Q�ƂȂ�܂��B����͂g�����O�D�T�ɑ��ă��g�����O�D�S�i�g�����g�����O�D�P����j�̂��߁A���[�������z���̉e���Əd�ʔz���̉e�����S�F�P�ŕ\��邽�߂ł��B�܂�g�[�^���őO��Q�O�O�������̍��E�d�ړ��̂����P�U�O�������̓��[�������z���ɂ���Č��܂�A�c��̂S�O�����������d�ʔz���ɂ���Č��܂�Ƃ������Ƃł��B���[�������O��z�����U�O�F�S�O�Ȃ�A���̉e���ɂ�鍶�E�d�ړ��ʂ͂P�U�O�����������̊����ŕ������X�U�������F�U�S�������ƂȂ�A���̂Ƃ��d�ʔz�����T�O�F�T�O�Ȃ�c��̂S�O�����������̊����ŕ����ĂQ�O�������F�Q�O�������B�g�[�^�����č��E�d�ړ��̑O��z���́A�i�X�U�{�Q�O�j�������F�i�U�S�{�Q�O�j�������ƂȂ�킯�ł��B���[�������z�����T�O�F�T�O�ŁA�d�ʔz�����U�O�F�S�O�̏ꍇ�́A�i�P�U�O�~�O�D�T�{�S�O�~�O�D�U�j�������F�i�P�U�O�~�O�D�T�{�S�O�~�O�D�S�j���������P�O�S�������F�X�U�������ƂȂ�܂��B
�\4.3�A���[���Z���^�[���̑O��o�����X��U�����ꍇ�̍��E�d�ړ���
|
�f�� |
�f�� |
�v�� |
�v�� |
�g�� |
�g�� |
���g�� |
��deg |
���v�� |
���v�� |
|
2500 |
2500 |
500 |
500 |
0.5 |
0.5 |
0 |
0 |
100 |
100 |
|
�� |
�� |
�� |
�� |
0.8 |
0.2 |
�� |
�� |
160 |
40 |
|
�� |
�� |
�� |
�� |
0.2 |
0.8 |
�� |
�� |
40 |
160 |
|
2500 |
2500 |
500 |
500 |
0.25 |
0.25 |
0.25 |
1.43 |
100 |
100 |
|
�� |
�� |
�� |
�� |
0.4 |
0.1 |
�� |
�� |
130 |
70 |
|
�� |
�� |
�� |
�� |
0.1 |
0.4 |
�� |
�� |
70 |
130 |
|
2500 |
2500 |
500 |
500 |
0.4 |
0.1 |
�� |
�� |
100 |
100 |
|
3000 |
2000 |
�� |
�� |
�� |
�� |
�� |
�� |
140 |
60 |
|
2500 |
2500 |
600 |
400 |
0.357 |
0.089 |
�� |
�� |
135.7 |
64.3 |
�Ō�Ƀ��[���Z���^�[���̑O��o�����X�̉e���ɂ��Đ����Ă͂߂Ă݂܂��傤�B�\4.3�̏�R�i�̓��g�����O�łg���Ƃg�����O�D�W���F�O�D�Q���i�W�O�F�Q�O�j�ɂ����ꍇ�ŁA���E�d�ړ��͑O���{�U�O�����łP�U�O�����A��낪�|�U�O�����łS�O�����ƂȂ�܂��B�܂�O�q���B�̐����̂悤�ɍ��E�d�ړ��ʂ͂v���~�g�����T�O�O�~�O�D�W�A�v���~�g�����T�O�O�~�O�D�Q����W�O�F�Q�O�̊����ɂȂ邱�Ƃ��킩��܂��B
����A�^�̂R�i�̂悤�Ƀ��g�����O�D�Q�T�łg���Ƃg�����O�D�S���F�O�D�P���i�W�O�F�Q�O�j�ɂ���ƍ��E�d�ړ��͑O���{�R�O�����łP�R�O�����A��낪�|�R�O�����łV�O�����ƂȂ�܂��B��̗�ɑ��Ĕ����́{�R�O�A�|�R�O�����ƂȂ�̂́A���g�����O�D�Q�T�łg���̂P�^�Q�̂��߁A���E�d�ړ��̑O��z���ɑ���u���[�������z���v�Ɓu�d�ʔz���v�̉e���͂��ꂼ�ꔼ�����\��邱�ƂɂȂ�܂����A�u���[�������z���̉e���v�̓C�[�u���ŁA�c�蔼���ɑ��Ăg���Ƃg�����v���~�g���Ƃv���~�g���̌`�ʼne�����邽�߁A��̗�Ɠ������g���F�g�����W�O�F�Q�O�Ƃ��Ă����̉e���͔��������\��Ȃ��i�T�O�F�T�O���W�O�F�Q�O�������̂ɑ��Ĕ����̂U�T�F�R�T�ɂȂ�j�Ƃ������Ƃł��B
���R�i�̓��g�����O�D�Q�T�̂܂܁A�g���F�g�����W�O�F�Q�O�Ƃ������̂���ɁA���[�������z���Əd�ʔz���̈�������ꂼ��U�O�F�S�O�ɐU�����ꍇ�ł��B���g�����P�^�Q�g���ł����̏ꍇ�͂g���Ƃg�����������Ȃ��̂Łu���[�������z���v�Ɓu�v���~�g���F�v���~�g���v�̉e�������ꂼ�ꔼ�����邱�ƂɂȂ�܂��B�ŏ��̗�̓��[�������z�����U�O�F�S�O�ł�����A�S�d�ړ��ʂQ�O�O�������̂����̔����̂P�O�O�������ɂ��Ă͂U�O�������F�S�O�������ō��E�d�ړ����邱�ƂɂȂ�܂��B�c��̂P�O�O�������͏d�ʔz�����T�O�F�T�O�Ȃ̂ŁA�i�T�O�~�W�O�j�F�i�T�O�~�Q�O�j���W�O�������F�Q�O�������ō��E�d�ړ����邱�ƂɂȂ�A���v�Łi�U�O�{�W�O�j�������F�i�S�O�{�Q�O�j�������ƂȂ�܂��B
�Ō�̗�ł̓��[�������z���͂T�O�F�T�O�ŏd�ʔz�����U�O�F�S�O�A�g���F�g�����W�O�F�Q�O�i�d�S�ʒu���ς���Ă���̂Ń��g�������킹�邽�ߐ������ς���Ă���j�Ȃ̂ŁA���E�d�ړ��ʑS�̂Q�O�O�������̂����̔����̂P�O�O�������͂T�O�������F�T�O�������A�c��̂P�O�O�������́i�U�O�~�W�O�j�F�i�S�O�~�Q�O�j���U�F�P���W�T�D�V�������F�P�S�D�R�������̑O�㊄���ō��E�d�ړ����邱�ƂɂȂ�A���v�Łi�T�O�{�W�T�D�V�j�������F�i�T�O�{�P�S�D�R�j�������ƂȂ�܂��B
���ۂɂ̓��[���Z���^�[���̓[���łȂ����Ƃ������A�O��ňقȂ�A���d�S���̕��������̂����ʂȂ̂ŁA�O��ւ̍��E�d�ړ��ʂ́A�����̃~�b�N�X�Łu���[�������O��z���v�u�O��d�ʔz���v�u�d�S���ɑ���O��̃��[���Z���^�[���v�ɂ�茈�܂��Ă���Ƃ������Ƃł��B
��������ƁA�w���E�d�ړ��̑O��z���ɑ��ẮA�d�S���ɑ��郢�g���̊����Łu���[�������O��z���v�Ɓu�O��d�ʔz���v�̉e���̊��������܂�A��҂͂���Ɍ����ɂ͑O��̃��[���Z���^�[���̉e�����āA�u�v���~�g���Ƃv���~�g���̊����v�Ō��܂�x�Ƃ������ƂɂȂ�܂��B�Ⴆ�A�O�֑��̍��E�d�ړ���傫�����ăA���_�[�X�e�A�X�����������悤�Ǝv���A�u�O��d�ʔz���v�̓t�����g���ɂ��A�u���[�������O��z���v���t�����g���ɁA�u�O��̃��[���Z���^�[���v�̃o�����X�̓t�����g����������Ηǂ��Ƃ������ƂɂȂ�܂��B�܂��u�d�ʔz���v�̉e�����u���[�������z���v�̉e���������o�������ꍇ�ɂ́u�O��̃��[���Z���^�[���v��Ⴍ���ă��g����傫������Ηǂ��Ƃ������Ƃł��B
�@���A�Ō�́u�O��̃��[���Z���^�[���̃o�����X�̓t�����g����������v�ɂ��ĕ⑫����ƁA����͎��i�S�|�Q�j�A���i�S�|�R�j����킩��悤�ɗႦ�t�����g�̍��E�d�ړ��ʃ��v���̓T�X�y���V�����̃��[�������~�ӕ��ƃ^�C�����������Ă���R�[�i�����O�t�H�[�X�~���[���Z���^�[���̃��[�����g�����v���~�s���Ŏ����Ȃ���Ȃ�Ȃ����Ƃ��痝���ł���Ǝv���܂��B���[���Z���^�[�����O�オ�肾�ƃt�����g�������オ��A���A�ɂ̂�������悤�ȑΊp���[������̃C���[�W�ŁA���A�̍��E�d�ړ����t�����g���傫���Ȃ�悤�Ɋ��o�I�Ɏv����������������邩������܂��A����͑Ίp���[���ɂ��d�S�_���w�I�ɑO��ړ����镪�̃C���[�W�ł���A���[�������O��ɌX���Ă����ꍇ�̃��[���ɔ����O��d�ړ��ʂ̓��[���Z���^�[���̌X�����ƂƂ���ƁA
�@�v�E���g���E�������ƁE��������
�ƂȂ�A�ӂ�Ƃ������ȗ̈�ł͂��������d�Ȃ��Ă��邱�Ƃ�����킩��悤�ɁA�ɂ߂Ĕ����Ȓl�i���O�Ɉړ��j�ƂȂ�܂��B�R�[�i�����O�t�H�[�X�~���[���Z���^�[���̃��[�����g�ɂ��e���ɑ��Ė����ł���I�[�_�[�Ƃ������Ƃł��B
�@�A�����[���Z���^�[���̓T�X�y���V�����̃W�I���g���ɂ���Č��܂�A���̃W�I���g������ɂ͗l�X�ȗv�f���֘A���邽�߁A�O�E��̍��E�d�ړ��ʂ��R���g���[�����邾���̂��߂Ƀ��[���Z���^�[����ݒ肷��Ƃ������Ƃ͎��ۂɂ͂���܂���B
�����̍��ڂց��@�@���ڎ��ց��@�@���g�n�l�d�ց�