<2-3、前後輪タイヤスリップ角とステア特性の関係②>
作図による説明で何となくだまされたような気になった人がいたら、追加の説明をしてみましょう。定常円旋回中、前輪位置と重心位置、そして後輪位置の進行方向がそれぞれ違っているのは旋回中心と結んだ線と直角な線をそれぞれ考えればわかるのですが、ヨーレイトωを使って理解することもできます。図2.6左のように、車両が左旋回しているということは反時計回りのヨーレイトω(角速度)をもって運動しているということです。
![]()
![]()
従って前述の<1-3、旋回のもう少し詳しい説明>の項のところでも説明したように、重心点を基準に考えると車両の前の方はω分だけ左方向に回され、後ろの方は右方向に振り出されていることになります。従って重心点の進行速度のベクトルを基準に前輪位置での進行方向はベクトルの向きがLf×ω分だけ左に、後輪位置での進行方向はLr×ω分だけ右に向いているというわけでしたね。
後輪は基本的には車体に固定されているので、後輪位置での車体の進行方向と車体の成す角が後輪タイヤスリップ角となり、前輪では前輪位置での車体の進行方向と前輪実舵角の成す角が前輪タイヤスリップ角となります。
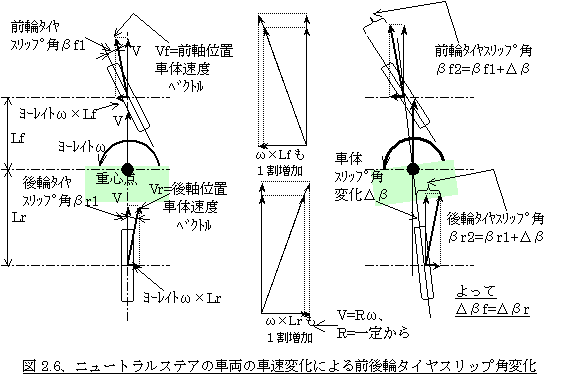
さてここでニュートラルステアの車両があったとして、この車の車速Vが仮に1割増加したとします。後輪位置の速度ベクトルはVが1割増えたことにより車両前方方向に1割伸びます。ところでこの車両はニュートラルステアなのでVが増えてもRは一定ですから、V=R×ωの関係からωも1割増加します。するとこの分で後輪位置に右方向にのっているLr×ωの速度成分も1割増えることとなり、結局βrは変わらないということになります(図2.6中央下参照)。これでは旋回加速度が増えた分に対応するコーナリングフォースの増大を達成するためのスリップ角の増加が図れないわけですからその分車体全体を旋回内側に向けて、すなわち車体の進行方向を車体に対して右向きに増やしてその分の後輪位置スリップ角を増やすことになります。前輪でも同様で、車速Vの増加割合とLf×ωの増加割合は同じでこの分のスリップ角は変化無し(図2.6中央上参照)で、車体全体を内側に向ける分の速度ベクトルの増減は車体のどの位置でも共通なので、前輪位置の進行方向もその分右に向くこととなり、前輪のタイヤスリップ角も後輪と同じだけ増加します。従ってβf、βrの増加量Δβf、ΔβrはΔβf=Δβr=Δβとなります(図2.6右参照)。常にΔβf=Δβrが成り立つということは、常にβf=βrということです。
逆にもし車速を増やしたときの前後輪スリップ角の変化がΔβf>Δβrとなる車があるとすると、どういうことになるでしょうか。
車体全体が内側に向いた分は前述のように前輪にも後輪にもタイヤスリップ角が同じだけ増えるように作用するので、Δβf>Δβrとなるためにはヨーレイト分の横速度と車速の割合が変化したということになります。車速(前後速度成分)とヨーレイトによる横速度分で作られるタイヤスリップ角は、後輪では増える方向、前輪では減る方向なので、すなわち車速の増加分に対してヨーレイトがそれほど増えなければこの量が減り、後輪のタイヤスリップ角が減って前輪のタイヤスリップ角が増えることになるわけです。つまり後輪ではVの増加ほどにはLr×ωやLf×ωが増えず、それによりΔβf>Δβrとなるわけです。「車速の増加分に対してヨーレイトがそれほど増えない」となるのはどういうことかというと、V=R×ωの関係から旋回半径Rが増大したということです。
そして、ある車速から増速したとき常にΔβf>Δβrとなるということは、どのような車速でも常にβf>βrということです。
よってβf>βrの車は前輪舵角一定で車速を上げると旋回半径Rが増大する、すなわちアンダーステアの車両であるということです。
感覚的な表現をすれば、アンダーステアの車両とは重心回りのヨーイングモーメントが釣り合って定常円旋回するとき、必要なスリップ角が常に後輪の方が前輪より小さくてすむ、すなわちバランス上“後輪のポテンシャルの勝った車両”と考えるとわかりやすいかもしれません。
尚、ある車重の車がある旋回加速度である半径の定常円旋回をしているときの車体(重心位置)のスリップ角(どれぐらい旋回内側あるいは外側を向いているか)は、ひとえに重心点の位置(ホイールベースとそれに対する後軸~重心点距離)と後輪のタイヤ特性(コーナリングパワー:但し後述する、スリップ角に対するコーナリングフォースの非線形性がない場合)で決まります。ここでコーナリングパワーとはタイヤが「スリップ角1°あたり発生するコーナリングフォース」のことです。
何故なら後輪操舵装置を備えた車を除き、ほとんどの車では後輪は(サスペンション特性によるトー角変化等を除き)車体に固定されているため後輪にスリップ角を与えようとすれば後輪位置の車体にスリップ角を与えるしかないからです。すなわち旋回加速度が決まれば前後輪トータルのコーナリングフォースが決まり、さらに“重心点まわりのヨーイングモーメント=0”という条件から、後輪が受け持たなければならないコーナリングフォースは一義的に決まります(=後軸荷重×旋回G)。そのコーナリングフォースを後輪のそのタイヤ特性で発生するために必要なタイヤスリップ角(後輪に必要なコーナリングフォース/後輪のコーナリングパワー)=“後輪位置での車体スリップ角”が決まります。すると重心点ではその値から“重心~後軸間距離にヨーレイトをかけた分”を割り引いた角度が重心点での車体スリップ角となるわけです。また、重心点の車体スリップ角は旋回加速度が小さいときは旋回接線方向に対して車体が外向きであり、次第に内向きとなります。
ちなみに上記は旋回加速度と半径(そして必然的に車速)がわかっていた場合で、旋回加速度と前輪実舵角と車速がわかっている場合も定常円旋回の状態は一義的に決まりますが、この場合は車体スリップ角は前輪側の情報(前輪のタイヤコーナリングパワー)がわからないと決まりません(後述の<6-1、定常円旋回の運動方程式>の式(6-9)参照)。これは旋回状態を旋回半径の代わりに前輪実舵角を用いて定義しているためです。