<1−3、旋回のもう少し詳しい説明>
先程の説明で満足されなかった方は、少々ややこしいですが我慢して読んで下さい。
まず、旋回により車体に固定された後輪にタイヤスリップ角が付くことを最初に理解しましょう。一部の本などでは、後輪にスリップ角を付けるには車体を旋回内側に向けるしかないというような表現がありますが、車体全体を旋回内側に向けなければならないと解釈するのは正確ではありません。そもそも車体の旋回接線方向に対する角度(車体の向きと車体の瞬間的な進行方向との成す角度=車体スリップ角)は車体の部位によって異なります。車体は一つなのに車体の進行方向がそれぞれ違うってどういうことでしょうか。図1.8をもう一度みて下さい。この図では各部の角度をはっきり見せるため、旋回半径が極端に小さく誇張して書かれていますが、前軸位置では車体の進行方向に対して車体の方向が外を向いているのに対して、後軸位置では進行方向が外、すなわち車体が内側を向いていることがわかると思います。さらにこのとき重心点では両者の中間ぐらい、この例ではほぼ進行方向と車体の向きが同じぐらいか、若干進行方向に対して車体が外を向いていることも見て取れると思います。
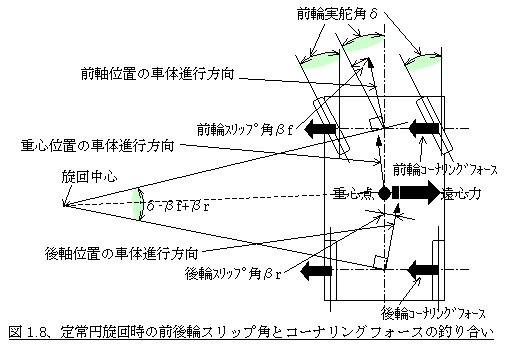
一般的に注釈無しで車体のスリップ角というと、重心点位置での車体の進行方向と車体の向きとの成す角度をいいますが、上記からわかるように旋回中、仮に重心位置の車体スリップ角が=0でも後軸位置では車体が進行方向に対して旋回内向きに車体スリップ角が付いているということになります。もっというと旋回加速度の低い(半径が大きいか、車速が低い)領域では(重心点の)車体スリップ角は車体が進行方向に対して外を向いていて、旋回加速度が上がるにつれてやがて=0となり、さらに旋回加速度を上げるとようやく内側を向くのです。
さてどうして重心点位置の車体が進行方向に対して旋回外側を向いていても後軸位置では内側を向いていることになるのでしょうか。図1.8の作図から直感的にも理解できると思いますが、ここでは別の方向から説明をしましょう。図1.10を参照してください。
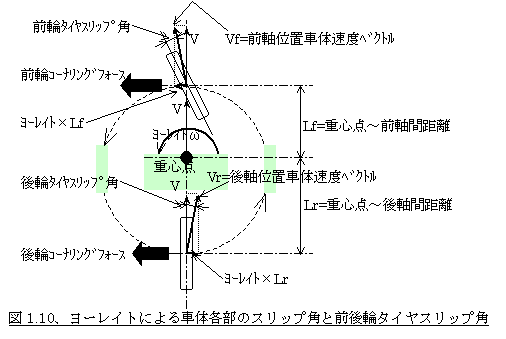 |
この図では簡略のため左右輪は1つにまとめて前後輪2輪だけで表現していますが、車体にヨーイングモーメントが入力されて例えば左回りにヨーレイトが発生すると、そのヨーレイトにより後軸位置では車体の横方向の速度成分が「ヨーレイト×Lr(重心点〜後軸間距離)」だけ相対的に右方向に加わり、前軸位置では逆に「ヨーレイト×Lf(重心点〜前軸間距離)」だけ相対的に左方向に加わるわけです。従って仮に重心点の車体スリップ角が=0でも、この分で後軸位置での車体スリップ角は内向き(瞬間的な進行方向は車体に対して外向き)に、前軸位置では車体スリップ角は、車体が瞬間的な進行方向に対して旋回外向きになるわけです。尚、図の例では前輪はこの車体スリップ角分より前輪実舵角の方が更に内側を向いているので、内向きにコーナリングフォースを発生するようなタイヤスリップ角が付いているわけです。
さて話をコーナリングに戻すと、ハンドルを左に切って前輪にスリップ角が付きコーナリングフォースが発生すると左回りのモーメント(すなわち左回りのヨー角加速度)が車体に作用します。すると車両は左旋回を始め、その旋回半径が無限大(直進)から徐々に小さな半径になっていきます。つまり左回りの回転速度(ヨーレイト)が車体の重心点廻りに発生し、どんどん大きくなるわけです。しかし先程説明したように、このヨーレイトで車両の重心より前方では左方向の速度成分が、後方では右方向の速度成分が乗ることにより後輪では旋回内向きのタイヤスリップ角が発生して増える一方、前輪では前輪舵角により発生したタイヤスリップ角を減らす方向に作用するわけです。そうなると最初の左回りのモーメントをそれぞれ減らす方向に作用することになりますが、この作用はヨーイングモーメントのアンバランスがある限り、すなわちヨーレイトが増大し続ける限り作用します。このため車速・ハンドル舵角=前輪の切れ角が一定であれば、(そして後で説明するステア特性がオーバーステアの車両のある舵角、車速以上の領域でない限り)いずれ前輪のコーナリングフォースによる重心点まわりのモーメントと後輪による分が釣り合って合計のモーメントが0になるところでヨーレイトが落ち着きます。つまり前輪のコーナリングフォースに重心点〜前軸間距離をかけたものと、後輪のコーナリングフォースに重心点〜後軸間距離をかけたものは等しく釣り合っている状態です。すなわち重心まわりのヨーイングモーメント=0、ヨー角加速度=0となっている状態です。ちなみにヨーレイトはこの状態で0ではなく、定常円旋回しているとき一定の値を持ちます。空からこの車を見下ろせば1周回る毎に1回転向きを変えるわけで、車に注目してみればある一定の速度でヨーイング方向に向きを変えているわけです。
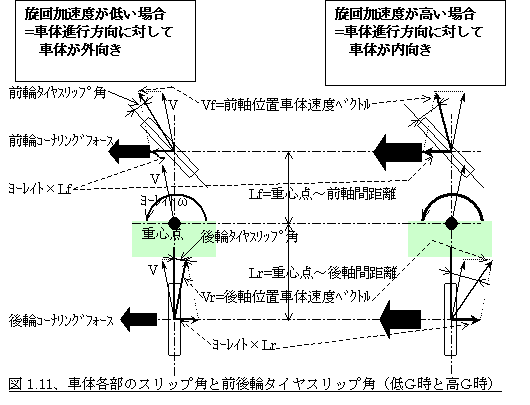
また本来、前後輪のスリップ角はこのヨーレイトにより発生した横方向の速度のみによって生ずるのではなく、重心点の車体スリップ角も加わって形成されます。従って後輪ではこの「重心点の車体スリップ角にヨーレイトによる横速度分を足した分」、前輪は「重心点の車体スリップ角にヨーレイトにより横速度分を引いた分と前輪舵角との差」がそれぞれのタイヤスリップ角となります。参考のため図1.11に旋回加速度が低い場合=重心位置の車体進行方向(旋回接線方向)に対して車体が旋回外向きの場合と、旋回加速度が高い場合=進行方向に対して車体が旋回内向きの場合の2つの例での、各位置の車体スリップ角とタイヤスリップ角の関係を示しておきます(図1.11参照)。ただここでは、この重心点の車体スリップ角分は前輪にも後輪にも共通して付いているため、このヨーイングモーメントの収束の話と分離して考えた方がわかりやすいと思います。
 |
それはともかく、最初に前輪で発生したコーナリングフォースにより車体にモーメントのアンバランスが発生し車両は旋回しはじめ、このヨーイングモーメントのアンバランスによって生じた分のヨーレイトが前輪のスリップ角を減らす方向に、後輪のスリップ角は増やす方向に作用してアンバランスを是正することにより、ある状態でヨーイングモーメントが0となり、一定の旋回状態(定常円旋回)になる。そしてそのとき前後輪のコーナリングフォースの和と、その質量の車がその車速、その旋回半径で旋回するときの遠心力(求心力)とが釣り合って旋回しているということは何となくおわかり頂けたでしょうか。そしてこの時の前・後輪それぞれのコーナリングフォースは、高校で習ったF=m×αから、前軸重・後軸重(本当は質量)に旋回加速度をかけた値であり、旋回半径は同じくα=V2/Rから、車速の2乗を求心加速度で割った値であり、ヨーレイトはω(角速度)=V/Rから、車速を旋回半径で割った値となります。