<6−1、定常円旋回の運動方程式>
ここでいう運動方程式とは、簡単に言うと例のF=m×αというやつです。また、旋回に関するものなので、車両の横方向の運動方程式とヨーイング方向の運動方程式の2つをたてます。面倒なので左右輪は1つとして、前後2輪で考えます。
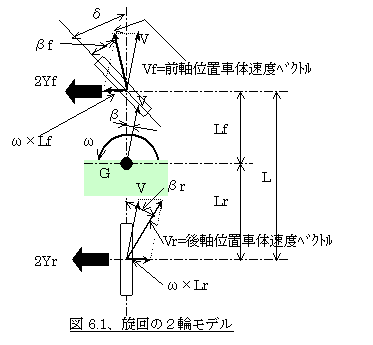 |
具体的には、M:車両質量、I:車両のヨーイング慣性モーメント、G:車両重心点、V:車速、δ:前輪舵角、β:重心位置スリップ角、βf:前輪タイヤスリップ角、βr:後輪タイヤスリップ角、Yf:前輪のコーナリングフォース(1輪あたり)、Yr:後輪のコーナリングフォース(1輪あたり)、ω:ヨーレイト(旋回角速度)、L:ホイールベース、Lf:前軸〜重心点距離、Lr:後軸〜重心点距離、として
まず、横方向の運動方程式は円運動の加速度の式が
M×α=Fで、α=V×ω、F=2Yf+2Yrだから、
M・V・ω=2Yf+2Yr …(6−1)
(本来はM・V(dβ/dt+ω)=2Yf+2Yrなのだけれど、今は定常円旋回だからdβ/dt=0)
尚、何故本来はdβ/dtの項があるかというと、今車両がスリップ角βの向きにVの大きさの速度ベクトルをもっているとすると車両横方向にはβが微小であればV・sinβ≒V・βの速度をもっていることになります。仮にβが一定でなくdβ/dtの割合で変化しているとすると、横方向速度V・βもその方向にV・dβ/dtで変化している(すなわちV・dβ/dtの加速度をもっている)ことになるためです。但し今は定常円旋回なので車体スリップ角βは一定でdβ/dt=0となり、この項は出てきません。
次に、ヨーイング方向の運動方程式は、ヨー角加速度=dω/dtから
I×dω/dt=2・Lf・Yf−2・Lr・Yr
しかし、今は定常円旋回なのでヨーレイト一定、すなわちヨー角加速度がゼロ、つまり
dω/dt=0から
2・Lf・Yf−2・Lr・Yr=0 …(6−2)
ここで前後輪のコーナリングパワー(スリップ角1°あたりのコーナリングフォース)を
それぞれ、Kf、Krとすると、タイヤ(車体)スリップ角の符号の定義を「タイヤ(車体)進行方向に対するタイヤ(車体)の向き」と定義し、回転方向は上から見て反時計回りを正と定義しているので(<本文中の式の正負符号について>参照)
Yf=Kf・βf
Yr=Kr・βr
ここで図6.1から「前軸位置の車体スリップ角」=β−Lf・ω/V
(符号に違和感があるかもしれませんが、正のヨーレイトにより発生するLf・ω/V分はそれによって車体が相対的に時計回りに開くことになるので負)
タイヤスリップ角は「タイヤ進行方向に対するタイヤの向き」の定義に従い
βf=δ+(β−Lf・ω/V)}=δ+β−Lf・ω/V
よって、
Yf=Kf・(β−Lf・ω/V+δ) …(6−3)
同様に、「後軸位置の車体スリップ角」=β+Lr・ω/V
よって後輪タイヤスリップ角は
βr=0+(β+Lr・ω/V)=β+Lr・ω/Vから
Yr=Kr・(β+Lr・ω/V) …(6−4)
式(6−3)と式(6−4)を式(6−1)と式(6−2)へ代入すると
M・V・ω=2Kf(β−Lf・ω/V+δ)+2Kr・(β+Lr・ω/V)
…(6−5)
2Kf(β−Lf・ω/V+δ)Lf−2Kr・(β+Lr・ω/V)Lr=0
…(6−6)
式(6−5)と式(6−6)を整理すると
−2(Kf+Kr)β+{M・V2+2(Lf・Kf−Lr・Kr)}ω/V=2Kf・δ
…(6−7)
−2(Lf・Kf−Lr・Kr)β+2(Lf2・Kf+Lr2・Kr)・ω/V=2Lf・Kf・δ
…(6−8)
式(6−7)と式(6−8)をβ、ωについて解くと
1−M・Lf・V2/(2L・Lr・Kr)
β=−1・――――――――――――――――――――――――――――――――・δ・Lr/L
1−M・(Lf・Kf−Lr・Kr)・V2/(2L2・Kf・Kr)
…(6−9)
1
ω=――――――――――――――――――――――――――――――――・δ・V/L
1−M・(Lf・Kf−Lr・Kr)・V2/(2L2・Kf・Kr)
…(6−10)
※注)<6−1−1、式(6−7)、(6−8)からβ、ωを求める式の展開の詳細について>はこちら
また、R=V/ωから、
R={1−M・(Lf・Kf−Lr・Kr)・V2/(2L2・Kf・Kr)}・L/δ
…(6−11)
となり、車両諸元、タイヤ特性と車速Vを入れればそのときの「車体スリップ角β」及び「ヨーレイトω」、「旋回半径R」を求めることができます。
またここで、Vが微少の場合の旋回半径Rsは、式(6−11)のV2=0として
Rs=L/δ …(6−12)
となり、前に出てきた式(2−1)と同じになりましたね。