<10−4、内部力についての補足及びエンジンブレーキの場合のアンチリフト>
<10−2、アンチスカットジオメトリ>と<10−3、アンチダイブ、アンチリフトジオメトリ>の章においてサスペンションの仮想リンクの角度をホイールセンターで考えるのか接地点で考えるのか(ホイールトルクを除外して考えるのか、含めて考えるのか)という違いがありましたが、納得しづらいかもしれないのでここでもう少し詳しく説明したいと思います。多少くどいかもしれないので、前章までの内容で納得された方は読み飛ばして下さって構いません。
駆動時のスカットを考える場合には、その駆動トルクの源は駆動系の発生する駆動トルクであり、その反力(反トルク)は駆動系すなわちドライブシャフトからデファレンシャルギヤなどを経由して車体に入ります。つまりホイール(駆動)トルクはサスペンションに入力されないのでその分を分離しなければなりません。車輪はサスペンションに対して自由に回転できるので(つまりサスペンションはホイールセンター回りのトルクを受け止められないので)、接地点に働く前後力を受け止められるのはそのホイールセンターになるというイメージですが、別の言い方をするなら、車両全体の力とモーメントのトータルでみた場合に接地点に働く前後力からホイールトルクを差し引くとホイールセンターに働く前後力が残るということです。
一方でフットブレーキの場合は制動トルクを発生しているのはブレーキユニットであり、ブレーキユニットはサスペンションに固定されているのでその反力はサスペンションに入ります。ホイールトルクもサスペンションが受け止めるので、いわば車輪とサスペンションが一体になった形で接地点の前後力を受け止めるというイメージで捉えてもいいのですが、一旦ホイールセンターに働く前後力とホイールトルクに分解して、その両方がサスペンションに入力されると理解しても構いません。
ここで、最初に「接地点に働く前後力(駆動力もしくは制動力)をホイールセンターに働く前後力とホイールトルクに分解する」について、車両全体としてみた場合本当に同じになるのか確認して、次にフットブレーキの場合に接地点入力で考えたときと、ホイールセンターの前後力とホイールトルクに分けたときのそれぞれでサスペンションへの入力が同じ結果になるかどうかを簡単な例で確かめて見ましょう。
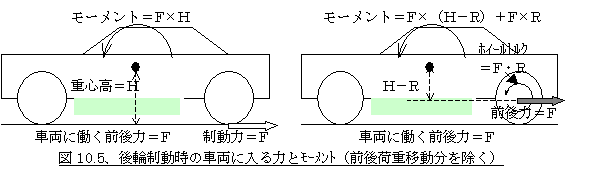 |
接地点に働く前後力をそのままで考えるか、ホイールセンターに働く前後力とホイールセンター回りのトルク分に分けて考えるかどうかは内部力に分解するかどうかの違いだけなので、車両全体で見た場合は同じになるはずです。確かめてみましょう。制動時を例に取ると、図10.5の左のように、後輪に制動力が発生している場合の力とモーメントを車両全体からみると(ここでは前後荷重移動分の上下力とその分のモーメントは除く)、後輪接地点に制動力=Fが発生しているので、車両全体に前後方向の力Fが働き、モーメントとしては重心点回りにF×Hのモーメントが働いていることになります。一方で図10.5の右のように、これをホイールセンターの前後力Fとホイールセンター回りのホイールトルクF×Rに分けて考えた場合の車両全体に働く力とモーメントのトータルも、車両に働く前後方向成分がFであることは同じで、重心点回りのモーメントはFが腕の長さH−Rに発生しているのでF×(H−R)とホイールトルクがF×Rで、合計は
F×(H−R)+F×R=F×H
となり図10.5の左の場合と同じ結果になります。
次にフットブレーキの場合の後輪について、ホイールセンターの前後力とホイールトルクに分けてその両方がサスペンションに入力されると考えても、「接地点」に制動力が入力されたと単純に考えても、結局同じ結果になることを確かめてみましょう。
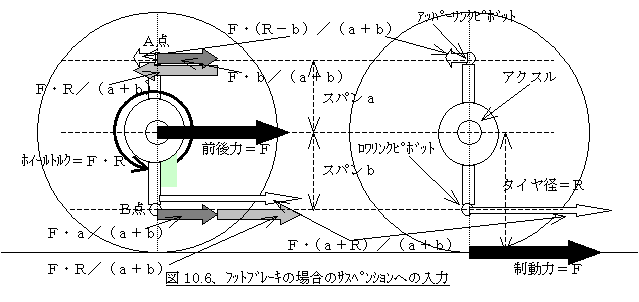
図10.6はフットブレーキング時の後輪の各部の力の様子を表したものです。分りやすいように今回はサスペンションを上下2つのリンクでアクスルを挟んだ形としています。A点、B点はそれぞれリンクのアッパーとロワのアクスル側ピポッドと思ってください。このA、B点への入力がどちらの場合も同じになるか確認します。サイドビューで見たホイールセンターからのスパンはアッパーがa、ロワがb、タイヤ径はRとし、後輪制動力をFとします。フットブレーキの場合、サスペンションにはホイールセンターに入る前後力とホイールトルクの両方が入力されます(図左側参照)。前者によるアッパーリンクの前後力をFU1、ロワリンクの前後力をFL1とすると、この分の前後力及びホイールセンター回りのモーメントの釣り合いから
FU1+FL1=F および FU1×a−FL1×b=0
これを解いて
FU1=F×b/(a+b) 、 FL1=F×a/(a+b) … (10−17)
となります(図中濃いグレーの矢印)。
次にホイールトルクF×R分のリンクへの入力を、アッパーをFU2、ロワをFL2とすると、この分のモーメント及び前後力の釣り合いから
FL2×b−FU2×a=F×R および FU2+FL2=0
これを解いて
FU2=−FL2=−F×R/(a+b) … (10−18)
(図中薄いグレーの矢印。FU2はマイナスだから左向き)
アッパーの合計FU、ロワの合計FLは、式(10−17)と(10−18)からそれぞれ
FU=FU1+FU2
=F×b/(a+b)−F×R/(a+b)
=−F×(R−b)/(a+b) … (10−19)
(図中白の矢印。「R−b」>0ならマイナスがつくからFと反対の左向き)
FL=FL1+FL2
=F×a/(a+b)+F×R/(a+b)
=F×(a+R)/(a+b) … (10−20)
(図中白の矢印。Fと同じ右向き)
一方、制動力=Fが接地点に入力されたと単純に考えた場合(図右側)のFU、FLは
FU+FL=F から FL=F−FU
また接地点回りのモーメントの釣り合いから
FU×(a+R)+FL×(R−b)=0
FL=F−FUを代入して
FU×(a+R)+(F−FU)×(R−b)=0
これを整理して
FU=−F×(R−b)/(a+b) … (10−21)
(図中白の矢印。「R−b」>0ならマイナスがつくからFと反対の左向き)
また、式(10−21)とFL=F−FUから
FL=F−FU=F+F×(R−b)/(a+b)
これを整理して
FL=F×(a+R)/(a+b) … (10−22)
となり(図右側の白の矢印。Fと同じ右向き)、当然ですが式(10−19)と(10−21)、式(10−20)と(10−22)は合致します。つまりフットブレーキの場合は両方ともサスペンションに入力されるので、前後力とホイールトルクとに分けて両方が入力されると考えても、分けずに接地点入力のままで考えても結局同じになります。
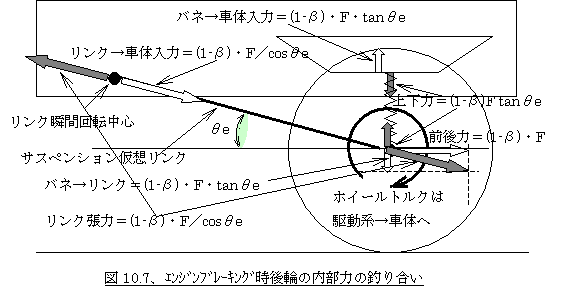 |
さて、せっかくここまで考えたのでついでにエンジンブレーキの場合のアンチリフトジオメトリについて考えてみます。エンジンブレーキの場合は制動力が小さいので実際上アンチリフトが問題になることはほとんどないのですが、この場合はホイールトルク分はサスペンションに入らないので、フットブレーキの場合のアンチリフトとの対比でどうなるかみてみましょう。
エンジンブレーキの場合はホイール(ブレーキ)トルクは駆動系が受け止めサスペンションには入力されないので、ホイールセンターの前後力分だけで考えます。よって図10.7のように仮想リンクと水平面との成す角(θe)はアンチスカットのときと同様、瞬間回転中心と「ホイールセンター」を結んだ線との角度となります。今、後輪(一輪当り)の制動力を(1−β)×Fとし(エンジンブレーキの場合は制動力は後輪だけなので単純にFとして考えてもいいのですが、前章のフットブレーキの場合の後輪と見比べるために揃えました)、エンジンブレーキング時のアンチリフトジオメトリによるストローク量をXr2とすると
Xr2=(1−β)×F×tanθe/Kr … (10−23)
前後荷重移動による後輪の荷重変化量=Xr1は、この場合制動力が後輪の(1−β)×Fだけなので
Xr1=(1−β)×F×H/(L×Kr) (左右片輪当たり)
となります。
したがって差し引きのリアの浮き上がり量Xrは、
Xr=Xr1−Xr2
=(1−β)×F×H/(L×Kr)−(1−β)×F×tanθe/Kr
=(1−β)×F/Kf×(H/L−tanθe) … (10−24)
となります。
ここでリアのリフト量をゼロにしようとするならば、式(10−24)から
(1−β)×F/Kf×(H/L−tanθe)=0
すなわち
H/L−tanθe=0 (ここで(1−β)は消えてしまいます)
から
tanθe=H/L … (10−25)
つまり、加速時のアンチスカットのような形となります。
整理すると、フットブレーキの場合とエンジンブレーキの場合のリフト量をゼロとするアンチリフトジオメトリは、<10−3、アンチダイブ、アンチリフトジオメトリ>の式(10−16)、及び式(10−25)から
フットブレーキの場合:tanθr=H/{(1−β)×L}
エンジンブレーキの場合:tanθe=H/L
となります。仮想リンクの傾きの定義が瞬間回転中心と「接地点」を結んだ線と水平との成す角(θr)なのか、瞬間回転中心と「ホイールセンター」を結んだ線と水平との成す角(θe)なのかが異なるのと、前後荷重移動のもとであるトータルの制動力が後輪分だけなのか前後輪分なのかで制動力リア配分(1−β)が出てくるかどうかが異なります。
前章の例、ホイールベース=2800mm、重心高560mm、制動力フロント配分=0.6の車両の場合で数字を当てはめてみると、
フットブレーキの場合のアンチリフトジオメトリは<10−3、アンチダイブ、アンチリフトジオメトリ>の結果から
θr≒26.6deg
エンジンブレーキの場合は、式(10−25)から
tanθe=H/L=560/2800=0.2
よって
θe≒11.3deg
となります(但し角度の定義が違うので単純比較はできません)。