<10−2、アンチスカットジオメトリ>
ここでは後輪駆動車において加速時に車体のリアの沈み込みを少なくする、サスペンションのアンチスカットジオメトリについて説明します。加減速時には前後荷重移動によって、車体がピッチング方向に姿勢変化することは<10−1、加減速時の姿勢変化はなぜ発生するか>で説明しましたが、サスペンションのジオメトリを工夫することによってこの姿勢変化を少なくしようというものです。
これを理解するときに、初めにタイヤに発生する力がどのような経路で車体に入力されるかを考える必要があります。図10.2のように、加速時にタイヤ接地点に発生している前引きの力(駆動力)はホイールセンターに働く前後力とホイールセンター回りのホイールトルクに分けて考える必要があります。何故ならホイールセンターに働く前引きの力はサスペンションを介して車体に入りますが、ホイール(駆動)トルクはサスペンションに対しては回転方向がフリーのためその反力はドライブシャフトからデファレンシャルギヤなどを介してそれを保持している車体に入力されるからです。つまりホイールトルク分はサスペンションには関係ないということです(詳しくは<10−4、内部力についての補足及びエンジンブレーキの場合のアンチリフト>参照)。
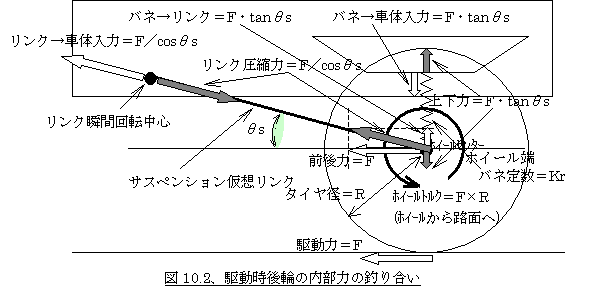 |
さて、図10.2ではリアサスペンションをサイドビューで見たとき、ある回転中心を持って動く1本の仮想リンクとホイールセンター上で上下方向に支えるバネに簡略化して考え、そのサイドビューで見た瞬間回転中心とホイールセンターを結んだ線(すなわち仮想リンク)と水平線との成す角度をθsとします。今、接地点に働く駆動力Fのうちサスペンションに入力される前後力Fがホイールセンターに働いているとすると、サスペンションリンクにはホイールセンターに働くFと水平方向において釣り合うように、リンク方向には「F/cosθs」の圧縮力が働き、その反力として同じ角度で図中左上向きに「F/cosθs」が車体に入力されます。ここで車体にはリンクの角度によって生じた「F×tanθs」という本来入力されていない上下力成分(斜めのうち上向きの分)が発生していることになりますが、サスペンションバネ経由で「F×tanθs」の下向きの力が車体に入力されて上下力のトータルが相殺されゼロとなってつじつまがあっています。このバネ経由で車体に入力されている上下力は、分りやすくいうと、リンクの端(ホイールセンター)を前方に引くとリンクは圧縮力を受けると共にその力によって下に下げられる方向に回転中心回りのモーメントを受けています。それをサスペンションのバネが上に引っ張ってリンクに働く回転中心回りにモーメントを釣り合わせることでリンクはある状態で静止しています。このバネの作用の反力として車体がバネに引かれて下向きの力を受けるイメージです。つまりホイールセンターの前後力によってリンクが下に引っ張られた分バネが伸びて、ホイールセンター(サスペンションリンク)を上に、車体を下に引っ張っているということです。これにより車体に入力される上下力のトータルはゼロとなり(ここで考えている入力は駆動力だけだからもともと上下力は入力されていない)、前後方向成分は「F/cosθs×cosθs=F」となります。つまりホイールセンターに働く前後力Fがサスペンションリンク方向の力とバネに象徴される上下方向の力に分散して車体に伝わったということになります。なお、ここで論じているのは駆動力のうちサスペンションに入力される力がどのような内部力に分解されて車体に作用するか、そのときその内部力の一部としてバネがどのように作用するかということで、駆動系経由で車体に入力されるホイールトルクや加速により生じる前後荷重移動による上下力の入力は、今この中には入っていません。
ここで注意すべきはサスペンションのリンクの傾きによってバネが伸び、内部力の上下方向成分を相殺している部分で、つまり具体的には、ホイール端バネ定数=Krとすると「F×tanθs」と釣り合う「Kr×Xr2」のXr2(ストローク)分、バネが相対的に伸びているということです。最初に説明したとおり、本来加速時には前後荷重移動によって車体はリアが沈み込みますが、このXr2分は逆に伸びるということになり、その分差し引きで沈み込み量が減るわけです。
ここでXr2は
F×tanθs=Kr×Xr2
から
Xr2=F×tanθs/Kr … (10−5)
となります。
もともとの前後荷重移動については、重心点回り働くモーメントが2×F×Hですから(接地点に働くFの左右輪合計と重心点からの腕の長さHで2×F×H)、後輪の荷重変化量は
後輪一輪当りの荷重変化量=F×H/L
(後軸の荷重変化量を2で割って一輪当りとするので、2×F×H/(L×2)から)
したがって、この分によるリアの沈み込み量はホイール端バネ定数で割って
前後荷重移動によるRrストローク量Xr1=F×H/(L×Kr) … (10−6)
となります。
式(10−5)と(10−6)から、トータルのストローク量Xr(沈み込み量)は差し引きで
Xr=Xr1−Xr2
=F×H/(L×Kr)−F×tanθs/Kr
=F/Kr×(H/L−tanθs) … (10−7)
となります。ここでリアのスカット(沈み込み)量をゼロにしようとするならば、式(10−7)から
F/Kr×(H/L−tanθs)=0
すなわち
H/L−tanθs=0
となります。
つまりリアのスカット量をゼロにしたい場合は
tanθs=H/L … (10−8)
となるような位置にサイドビューで見た瞬間回転中心が来るようにジオメトリを設定するということです。逆に万一θsがマイナス、つまり瞬間回転中心の高さがホイールセンターより下なら、このジオメトリ分、前後荷重移動による以上にリアのスカット量が増えることになります。
ちなみに荷重移動などによりサスペンションがストロークすれば当然瞬間回転中心の位置はそれにつれて厳密には変わっていきますが、数十ミリのストロークの範囲ではその変化は多くの場合微小なのでこの問題を扱う上ではイニシャル位置の瞬間回転中心について考えても実害はないと思います。また一般的にトレーリングアーム式などに対し、ダブルウィッシュボーン式やマルチリンク式のリアサスペンションの方がアンチスカットに対する自由度が大きいと言われるのは、ここで問題になるサイドビューで見た瞬間回転中心が仮想リンクの回転中心であるということで、トレーリングアーム式などは実際の揺動軸の位置でこの回転中心が決まるのに対して、例えばダブルウィッシュボーン式ならばサイドビューで見た上下2本のアームの揺動軸の延長線の交点が仮想回転中心となるため、スペースに制約されず比較的自由に瞬間回転中心の位置を設定できるためです。
ところで、アンチスカット率という言葉がありますが、これは式(10−8)の左辺tanθsの右辺に対する割合を言います。つまり
アンチスカット率=tanθs/(H/L) … (10−9)
アンチスカット率=1.0ならtanθs=H/Lで前後荷重移動によるストローク量とアンチスカットジオメトリによるストローク量が釣り合い、ちょうどリアがスカットしないジオメトリということになります。
ここで注意して頂きたいのは、アンチスカットジオメトリによるストローク量はあくまで内部力によるものであり、その分前後荷重移動量が減るわけではないということです。加減速による前後荷重移動量は<10−1、加減速時の姿勢変化はなぜ発生するか>の式(10−1)の通りであり、変わりありません。あくまでストロークが荷重移動分と内部力分で相殺されるだけなのです。
念のため付け加えておくと、後輪駆動車の前輪については、ここで説明したようなサスペンションジオメトリによって加速時の前後荷重移動に伴う浮き上がり量を低減することはできません。何故なら前輪には前後力(駆動力)が発生していないために前輪のサスペンションにそれによる内部力が働かないからです。同様に前輪駆動車の前輪については後輪駆動車のアンチスカットジオメトリと同じような考え方で前輪の浮き上がり量を低減することができますが、前輪駆動車の後輪については駆動力が発生していないのでサスペンションジオメトリで低減することはできません。4輪駆動車については前後輪ともこのジオメトリの考え方が適用できますが、注意する必要があるのは、前後荷重移動は前後輪トータルの駆動力によって荷重移動するのに対して前輪、後輪それぞれのサスペンションジオメトリによるストロークは前後それぞれの駆動力分のみによって起こるという点です(式(10−6)の前後力のトータルがFなら式(10−5)のFのところは「駆動力リア配分率」×Fとなる)。
さて、アンチスカットジオメトリについて前章と同じ車両の例で実際の数字を当てはめてみましょう。車両重量=1500kgf、ホイールベース=2800mm、重心高560mm、前後のホイール端バネ定数=2.0kgf/mmの車両が0.2Gで加速している例です。
式(10−8)からスカット量をゼロにするアンチスカットジオメトリは
tanθs=H/L=560/2800=0.2
よって
θs≒11.3deg
となります。
これを図10.2に当てはめて確認してみましょう。車輪に働く駆動力は
駆動力F=1500×0.2/2=150kgf
内部力の上下方向成分は
F×tanθs=150×0.2=30kgf
これによるサスペンションストローク量は式(10−5)から
Xr2=F×tanθs/Kr=30/2.0=15mm
前章の計算でこの場合の前後荷重移動によるサスペンションストローク量は15mmだったので、これを相殺し、スカットゼロとなることが分ります。重複ですが荷重移動量自体は前章のごとく30kgf(前後とも、左右一輪当り)であり、変わりません。