<10−3、アンチダイブ、アンチリフトジオメトリ>
アンチダイブジオメトリとは制動時に発生する車体のフロントの沈み込みを少なくするサスペンションジオメトリで、アンチリフトは制動時に車体のリアの浮き上がりを少なくするジオメトリのことです。制動時に生ずる前後荷重移動によって、そのままではフロントが沈み込みリアが浮き上がってしまうところを、サスペンションのジオメトリを工夫することによってこの姿勢変化を少なくしようというもので、アンチスカットジオメトリと考え方は同じです。
最初に制動に伴う前後荷重移動による前後輪のストローク量を整理しておくと、<10−2、アンチスカットジオメトリ>と向きが逆になるだけなので、前後荷重移動による前後輪のストローク量は、前後輪に働く制動力の(左右片輪ずつの)トータルをFとすると重心点回りに働くモーメントが左右片輪当りF×Hですから、前後のホイール端バネ定数をKf、Krとすると
前後荷重移動による前輪ストローク量Xf1=F×H/(L×Kf)(縮み)
… (10−10)
前後荷重移動による後輪ストローク量Xr1=F×H/(L×Kr)(伸び)
… (10−11)
となります。
次に<10−2、アンチスカットジオメトリ>の章と同じように、前後輪に発生している制動力がどのように車体に入力されるかを考えてみましょう。ここで今回は制動といってもエンジンブレーキではなくフットブレーキによる制動を考えます。
さて今、前後トータル(左右片輪ずつ)の制動力=Fで減速している状態を考えると、制動力フロント配分をβとして前輪にはβ×F、後輪には(1−β)×Fの制動力が発生しています。ここで前章と同様に仮想リンクの傾きをそれぞれθf、θrとしますが、ここで注意して頂きたいのは<10−2、アンチスカットジオメトリ>の章と違ってここではサイドビューで見た瞬間回転中心と「接地点」とを結んだ線を仮想リンクとして考え、それと水平線との成す角度をθf、θrとするということです。フットブレーキによるブレーキトルクはブレーキユニットを通じてサスペンションに入力されるためここでは前章とは異なり全てがサスペンション経由で入力されるため、前章のように前後力とホイールトルクに分けてホイールトルク分を除いて考える必要がなく、接地点の制動力そのままで考えるためです。(詳しくは<10−4、内部力についての補足及びエンジンブレーキの場合のアンチリフト>参照)
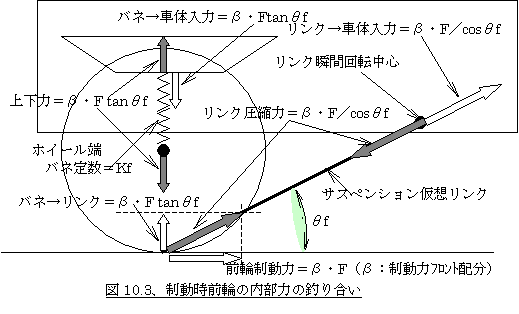
図10.3で前輪に着目するとタイヤ接地点に働く前輪制動力β×Fと水平方向において釣り合うように、仮想リンクにはリンク方向に「β×F/cosθf」の力が働き、その反力として同じ角度で図中右上向きに「β×F/cosθf」が車体に入力されます。そしてリンクの角度によって生じたこの力の上下方向成分、「β×F×tanθf」と、サスペンションバネ経由で下向きに車体に入力される「β×F×tanθf」が相殺しています。つまり<10−2、アンチスカットジオメトリ>の章の説明と同様に、この分バネが伸びてリンクを引っ張ってリンクに働く回転中心回りのモーメントをゼロにし、その反力として車体に下向きの力を伝えているイメージです。
このアンチダイブジオメトリによるストローク量をXf2とすると
β×F×tanθf=Kf×Xf2
から
Xf2=β×F×tanθf/Kf … (10−12)
となります。
もともとの前後荷重移動による前輪の荷重変化量=Xf1との差し引きのフロントの沈み込み量Xfは、式(10−10)と(10−12)から
Xf=Xf1−Xf2
=F×H/(L×Kf)−β×F×tanθf/Kf
=F/Kf×(H/L−β×tanθf) … (10−13)
となります。ここでフロントのダイブ(沈み込み)量をゼロにしようとするならば、式(10−13)から
F/Kf×(H/L−β×tanθf)=0
すなわち
H/L−β×tanθf=0
から
tanθf=H/(β×L) … (10−14)
となります。
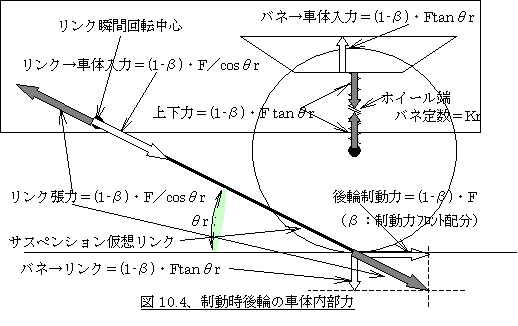 |
同様にリアについては(図10.4参照)、もともとの前後荷重移動による後輪の荷重変化量=Xr1との差し引きのリアの浮き上がり量Xrは、
Xr=F×H/(L×Kr)−(1−β)×F×tanθr/Kr
=F/Kr×{H/L−(1−β)×tanθr} … (10−15)
となります。ここでリアのリフト(浮き上がり)量はゼロにしようとするならば、式(10−15)から
F/Kr×{H/L−(1−β)×tanθr}=0
すなわち
H/L−(1−β)×tanθr=0
から
tanθr=H/{(1−β)×L} … (10−16)
となります。
つまりtanθf、tanθrがそれぞれ式(10−14)、(10−16)の値となるように瞬間回転中心の位置を選べば、制動時のノーズダイブ、リアリフト量はゼロになるということです。
また、アンチダイブ率、アンチリフト率については<10−2、アンチスカットジオメトリ>のアンチスカット率の式(10−9)と同様に、
アンチダイブ率=tanθf/{H/(β×L)}
アンチリフト率=tanθr/〔H/{(1−β)×L}〕
となります。ともに1.0ならノーズダイブ量、リアリフト量がゼロということです。
ここで今、車両重量=1500kgf、ホイールベース=2800mm、重心高560mm、前後のホイール端バネ定数=2.0kgf/mm、制動力フロント配分=0.6の車両が0.4Gで減速している例で数字を当てはめてみましょう。
式(10−14)から
tanθf=H/(β×L)=560/(0.6×2800)=0.333
よって、ノーズダイブをゼロとする前輪のアンチダイブジオメトリは
θf≒18.4deg
また、式(10−16)から
tanθr=H/{(1−β)×L}=560/(0.4×2800)=0.5
よって、ノーズダイブをゼロとする前輪のアンチダイブジオメトリは
θr≒26.6deg
となります。
これを検証してみましょう。
制動力のトータルは
1500×0.4=600kgf
左右片輪の前後合計は
600/2=300kgf
式(10−10)、(10−11)から
前後荷重移動による前輪ストローク量Xf1=F×H/(L×Kf)(縮み)
=300×560/(2800×2.0)
=30mm
前後荷重移動による後輪ストローク量Xr1=F×H/(L×Kr)(伸び)
=30mm
前輪アンチダイブジオメトリによる内部力の上下方向成分はβ×F×tanθfで、その分によるストローク量をXf2とすると式(10−12)から
Xf2=β×F×tanθf/Kf
=0.6×300×0.333/2.0
=30mm
後輪アンチダイブジオメトリによる内部力の上下方向成分は(1−β)×F×tanθrで、その分によるストローク量をXr2とすると
Xr2=(1−β)×F×tanθr/Kr
=0.4×300×0.5/2.0
=30mm
となり、それぞれ前後荷重移動によるストローク量と相殺することがわかります。
また、仮にθf、θrがそれぞれ半分の
θf≒9.2deg
θr≒13.3deg
であったなら、(θf、θrが微小と見なせる範囲では)ストローク量はそれぞれ半分となり、15mmずつしか相殺されないので残りの15mm分フロントはダイブしてリアはリフトすることになります。
なお、くどいようですがアンチダイブやアンチリフトをどういじっても前後荷重移動量は変わりません。この例では前後輪とも左右一輪当たり
1500×0.4/2×560/2800=60kgf
のままということです。
また、制動力フロント配分βを変更することによってもアンチダイブ、アンチリフトジオメトリが変わりますが、制動力配分は基本的にブレーキ性能から決まり、アンチダイブ、アンチリフトのためにこれを変えることは実際上ないと思います。