<10−1、加減速時の姿勢変化はなぜ発生するか>
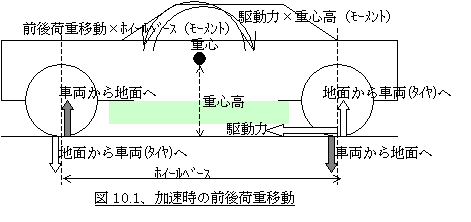
<9−1、タックインについて>でも説明したように、加減速時にはタイヤに駆動力、もしくは制動力が発生しているため重心点回りにピッチングモーメントが発生しており、このモーメントを打ち消すため前後輪の接地点に上下力が発生します。これが加減速時の前後荷重移動ですが(図10.1参照:白矢印の力が釣り合って車両に働くモーメントの和がゼロになる)、このときもしサスペンションのバネ定数やタイヤ縦バネ定数が無限大なら、前後荷重移動はしても車両はピッチ方向に姿勢変化することはありません。しかし実際にはあるバネ定数を持っているので、例えば加速時には荷重移動によって後輪は縮み、前輪は伸びる方向にバネがたわみ、車両はピッチングすることになります。
ここでタイヤのたわみについては、タイヤ縦バネ分はバネ定数がサスペンションバネ定数に対して相対的に一桁高いので無限大として無視すると、厳密には車両バネ上重量(サスペンションより上の車体重量=車両重量−サスペンションやタイヤなどのバネ下重量)分の前後荷重移動によりサスペンションがストロークすることになります。ここでバネ下重量はバネ上重量に対してかなり小さいので簡単のため無視して、バネ上重量=車両重量とすると、
まず加減速による前後荷重移動量は重心点回りのモーメントの釣り合いから
前後荷重移動量
=制駆動力のトータル×重心高/ホイールベース
=車体重量×加減速G×重心高/ホイールベース …(10−1)
そして、前後荷重移動による前後のサスペンションストローク量は
Frサスペンションストローク量(加速時は伸び、減速時は縮み)
=前後荷重移動量/(Frホイール端バネ定数×左右輪)
=制駆動力のトータル×重心高/(ホイールベース×Frホイール端バネ定数×2)
=車体重量×加減速G×重心高/(ホイールベース×Frホイール端バネ定数×2)
…(10−2)
Rrサスペンションストローク量(加速時は縮み、減速時は伸び)
=前後荷重移動量/(Rrホイール端バネ定数×左右輪)
=制駆動力のトータル×重心高/(ホイールベース×Rrホイール端バネ定数×2)
=車体重量×加減速G×重心高/(ホイールベース×Rrホイール端バネ定数×2)
…(10−3)
車両のピッチング角は
tan(ピッチング角)
=(Frサスストローク量+Rrサスストローク量)/ホイールベース
(Fr、Rrの伸び、縮みストローク両方をプラスとして) …(10−4)
となります。
(ここでホイール端バネ定数はスプリング単体ではなく、ブッシュ等の分も含めトータルをホイールストローク当りに換算したバネ定数のことです。)
ここで例として簡単な数字を入れてみましょう。今、車両重量=1500kgf、ホイールベース=2800mm、重心高560mm、前後のホイール端バネ定数=2.0kgf/mmの車両が0.2Gで加速しているとします。このときの前後荷重移動量とサスペンションストローク量、車両のピッチング角はそれぞれ、
式(10−1)から
前後荷重移動量=車体重量×加減速G×重心高/ホイールベース
=1500×0.2×560/2800
=60kgf(前後とも、左右輪トータル)
これを一輪当たりにすると
30kgf(左右一輪当り)前輪は減り、後輪は増えることとなります。
なお、このときに発生している駆動力は
車体重量×加減速G/2=1500×0.2/2=150kgf(一輪当り)
また、式(10−2)、(10−3)から
前後荷重移動によるサスペンションストローク量
=一輪当たり前後荷重移動量/(ホイール端バネ定数)
=30/2.0
=15mm 前後輪とも(前輪は伸び、後輪は縮み)
式(10−4)から
車両のピッチング角は
tan(ピッチング角)
=(Fr+Rrサスストローク量)/ホイールベース
=30/2800
よって、ピッチング角≒0.61deg
加減速時のピッチング方向の車両姿勢変化を小さくしようとするなら、式の内容から「車両重量を軽くする」、「重心高を低くする」、「ホイールベースを長くする」などがありますが、これらは基本的に他の要件で決まってしまうので、動かせないものとして考えれば、「前後サスペンションのバネ定数を高くする」ということになります。しかしそれでは例えばピッチング角を半分にするために前後のホイール端バネ定数を2倍、10分の1にするためには10倍にしなければならず、乗心地がとても硬くなるなど大きなデメリットが発生します。サスペンションのバネ定数を高くしないで姿勢変化量を抑えることはできないのでしょうか。
そこで出てくるのがサスペンションのアンチスカット、アンチダイブ(およびアンチリフト)ジオメトリと言われるものです。次からその具体的内容について説明します。