<9−2、タイヤの制・駆動力と横力、摩擦円の概念>
タイヤの制動力あるいは駆動力はどのようにして発生しているのでしょうか。
実は制・駆動力も横力と同じように路面との間にある種の「ずれ」がないと力を発生できません。横力の場合は進行方向のずれにより、トレッドゴムが路面から横方向に引っ張られて横力が発生しましたが、制・駆動力の場合はタイヤの回転速度が路面に対する進行速度と若干ずれていることにより、トレッドゴムが路面から前後方向に引っ張られて制・駆動力を発生するのです。
いま、タイヤに制・駆動力が働かず自由に転動しているとすると、タイヤの接地前端から後端までの移動速度とそれと接地する路面の移動速度が同じなので、図9.3の破線のようにトレッドゴムの付け根の速度と路面の速度にずれはなく、トレッドゴムに変位は発生しません。
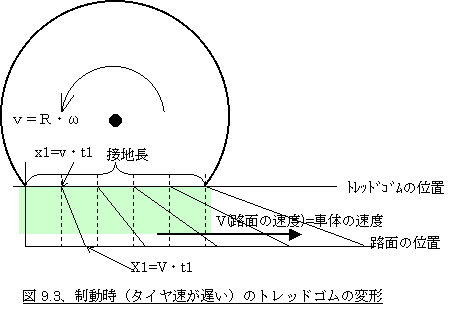
これに対し例えばブレーキをかけた状態のタイヤは、路面の速度(車両の速度)よりタイヤ(トレッドゴムの付け根)の回転速度が若干遅いので、両者の移動速度のずれによって図9.3の実線のように(この図は少し大げさですが)わずかにずれ(トレッドゴムの変形)が生じます。路面に着目して接地長全体を考えると、接地前端では踏み込んだばかりなのでトレッドゴムの付け根と路面にずれはありませんが、トレッドゴムの付け根の回転速度が路面の速度より遅いため、路面に対応するトレッドゴムの付け根は、接地後端になるにつれてずれが大きくなりトレッドゴムが引きずられて伸ばされる形になります。この相対変位にトレッドゴムの前後方向の剛性(バネ定数)をかけたものの総和がタイヤの発生する前後力になります。要するに路面とタイヤ自体のずれの方向は異なりますが、考え方はスリップ角の付いたタイヤの横力発生メカニズム(<7−1、タイヤ変形のモデルによる横力の説明>の項参照)と同じような考え方です。
では相対変位がどういう値か見てみましょう。いま路面の移動速度をVとし、トレッドゴム(の付け根)の移動速度をvとすると、路面上の接地前端からt1秒後の位置X1と、対応するトレッドゴム付け根の位置x1はそれぞれ、
X1=V・t1
x1=v・t1
だから、相対変位をΔX1とすると
ΔX1=(V−v)・t1
すなわち一般化して、接地前端からt秒後のxの位置の相対変位は、
ΔX=(V―v)・t …(9−2)
ここでX=V・tからt=X/Vだから
ΔX={(V−v)/V}・X …(9−3)
ここで、{(V−v)/V}の部分は路面の速度(車両の速度)とタイヤの回転速度の差の、路面の速度(車両の速度)に対する割合です。例えば車速(路面速)が100km/hで車輪速が90km/hならば
(100−90)/100=0.1
ということです。この(V−v)/Vをスリップ比(s)といいます。これはどのぐらいスリップしているかという値で、例ではs=0.1ですから10%スリップしているという意味です。
スリップ比sを用いて式(9−3)を書き直せば、
ΔX=s・X …(9−4)
となります。尚、車輪が完全にロックしていればv=0となり、s=1.0となります(100%スリップしている状態)。
次にこの相対変位を接地長全体について図に書けば、図9.4のようになります。縦軸は横力のときの横変位量ではなく、トレッドゴムの前後変位量です。スリップ比にしたがって接地後端へいくほど前後変位が大きくなるわけです。ここでスリップ比が小さいときは、スリップ角が小さいときの横力のときと同じように、滑り域は無視できるほど小さいのですが、スリップ比が大きくなってきて「相対変位×トレッドゴムの前後方向の剛性」が摩擦力を超えた点より後側は滑り域となることは、横力のときと同じです。
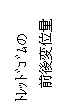
ちなみに駆動時もタイヤの回転速度と路面の速度が異なることにより、やはり同じように相対変位を生じます。この場合はタイヤの速度の方が速いのでそちらを基準に考えます。トレッドゴムの付け根が接地長だけ進む間に路面はそれほど進まないので、その相対変位はトレッドゴム(の付け根)の移動速度をvとし、路面の移動速度をV、トレッドゴム付け根の接地前端からのt1秒後の位置をx1、それと対応する路面上の位置をX1とすると、
x1=v・t1、X1=V・t1から
相対変位をΔx1とすると
Δx1=(v−V)・t1
すなわち
Δx=(v−V)・t
ここでx=v・tからt=x/vだから
Δx={(v−V)/v}・x …(9−5)
したがって駆動の場合のスリップ比sは
s=(v−V)/v
となります。もし車速が90km/hのとき、車輪がそれを上回る100km/hで回転していれば、
s=(100−90)/100=0.1
となり、もし車両が止まっていて(V=0)、車輪だけが回っている完全なホイールスピンの状態であれば、
s=(v−0)/v=1.0(100%スリップしている状態)
となります。
したがって相対変位はΔx=s・xとなり、これにトレッドゴムの前後方向の剛性をかけたものの総和が駆動力になるのは、制動の場合と同じです。
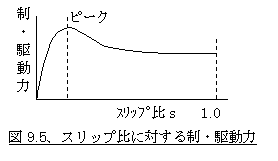
ところで、スリップ比に対する制動力あるいは駆動力の形は図9.5に示すような形になります。制動力あるいは駆動力がスリップ比がおおよそ0.1程度をピークに緩やかに減少するのは、それを越えると横力がスリップ角に対してサチュレートするのと同じようにトレッドゴムの変位が摩擦限界を超えるため三角形の頂点の高さが変わらず、面積が増えないためと思われます。またs=1の状態、制動ならばロック時の制動力、駆動なら完全なホイールスピンの状態の駆動力がピークより低いのは、この状態では接地長全域が滑っている状態のため、ピーク時の静摩擦力に近い状態に対して、値の低い動摩擦力になっているためと考えられます。
次に制・駆動力と横力が同時に働いたらどうなるか考えてみましょう。最初によく言われる摩擦円の概念について説明します。
タイヤにスリップ角が付くことでトレッドゴムに横方向の変位が生じ、それにトレッドゴムの剛性をかけた値の総和が横力でした。また、スリップ比が生じるとトレッドゴムに前後方向の変位が生じ、それにトレッドゴムの剛性をかけた値の総和が制動力(駆動力)でした。そしてそれぞれは変位が摩擦限界を超えるとピークを迎えることは先に説明しました。
今仮に最大変位がちょうど摩擦限界となるようなスリップ角で、最大の横力を発生しているタイヤにスリップ比を与えたら、横力が働いていないときの最大の制・駆動力をタイヤは発生するでしょうか?答えはNOです。トレッドゴムの接地後端に近いある一点を考えてください。この部分のトレッドゴムはスリップ角によって既にタイヤ〜路面間摩擦限界まで横方向に伸びています。この部分のトレッドゴムがスリップ比が付いたからといって更に前後方向に、横力の発生していないときのように変位できないのです。ゴムの変位は縦でも横でも斜めでも「変位×ゴムの剛性」が摩擦力と釣り合うところまでしか変位できません。最大変位が方向に係わらず摩擦力を限界とする以上、変位の総和にトレッドゴムの剛性をかけたものである制・駆動力や横力も、トータルで摩擦限界で決まる一定の範囲以上には発生できないということです。この範囲のことを摩擦円といい、このことを簡単に図示すると図9.6のようになります。
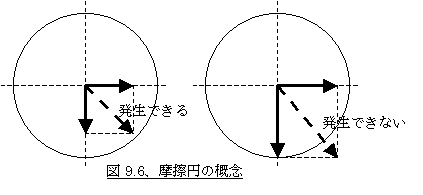
実際の運転状況でいうと、ある旋回状態を保ちながら例えば減速しようとしても、直線のときのように素速く止まることはできません。また極端な例では、フルブレーキングして前輪をロックさせ、タイヤが摩擦限界を超えた状態でハンドルを切っても車はまったく曲がりません。これらはタイヤが摩擦円の中しか力を発生できないからです。よく教習所などでコーナーでは不用意にブレーキをかけてはいけないと教えていますが、要するにタイヤに横力と制・駆動力を同時に発生させると、それぞれではまだ余裕のある範囲でも合計すると摩擦円を超えてしまうことになりかねず、車両が思いがけない挙動を示す危険性があるからです。