<6−2、スタビリティファクタについて>
ところで操縦安定性のポテンシャルを表す指標の一つとして、「スタビリティファクタ」というものがあります。それについて少し触れておきます。
定常円旋回時にアンダーステアの車両はβf>βr、ニュートラルステアはβf=βrオーバーステアはβf<βrであることは先に述べました。
ここで式(6−2)から
2・Lf・Yf−2・Lr・Yr=0
また、Yf=Kf・βf、Yr=Kr・βrからこれを代入して
Lf・Kf・βf−Lr・Kr・βr=0 …(6−13)
となりますが、このときβf=βr(ニュートラルステア)であれば
Lf・Kf−Lr・Kr=0
βf>βr(アンダーステア)であれば
Lf・Kf−Lr・Kr<0
βf<βr(オーバーステア)であれば
Lf・Kf−Lr・Kr>0
となります。ここで旋回半径の式(6−11)
R={1−M・(Lf・Kf−Lr・Kr)・V2/(2L2・Kf・Kr)}・L/δ
を考えるとオーバーステアのとき、すなわち
Lf・Kf−Lr・Kr>0のとき、旋回半径RはVがある値で=0となることがわかります。この速度以上では前輪舵角一定では旋回できないということです。このときのVは上記R=の式から
1−{M・(Lf・Kf−Lr・Kr)/(2L2・Kf・Kr)}・V2=0
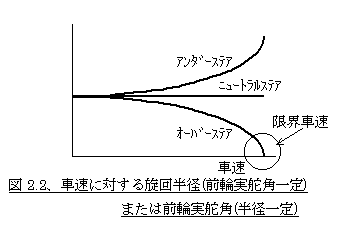
となるVです。この限界車速は(Lf・Kf−Lr・Kr)が小さいほど(つまりオーバーステアが弱いほど)、ホイールベースLや前後輪のコーナリングパワーKf、Krが大きいほど、高くなります。これは<2−1、ステア特性の定義>の項に出てきた、下に示す図2.2の円内に当たります。ニュートラルステアやアンダーステアではこのような限界車速は存在しません。
ニュートラルステアでは、Lf・Kf−Lr・Kr=0から
R={1−M・(Lf・Kf−Lr・Kr)・V2/(2L2・Kf・Kr)}・L/δの
1−M・(Lf・Kf−Lr・Kr)・V2/(2L2・Kf・Kr)は常に1となり、旋回半径Rは常に
R=L/δ
で一定となります。
また、アンダーステアの場合は、Lf・Kf−Lr・Kr<0ですから、車速Vの増加に伴い、
1−M・(Lf・Kf−Lr・Kr)・V2/(2L2・Kf・Kr)は増加していき、
旋回半径Rは車速の増加に伴い大きくなっていくことになります(図2.2参照)。

そこでこの「1マイナス」の後の部分のV2の係数をスタビリティファクタといい、操安性能を表す指標の一つとして使われます。
スタビリティファクタ=−M・(Lf・Kf−Lr・Kr)/(2L2・Kf・Kr)
スタビリティファクタは、ホイールベースLや前後輪のコーナリングパワーKf、Krが大きいほど高く、ステア特性(Lf・Kf−Lr・Kr)がアンダーステアなほど(負の値が大きいほど)大きくなります。そしてスタビリティファクタはアンダーステアでは正の値、ニュートラルステアでは0、オーバーステアでは負の値となります。