���R�|�R�A���E�d�ړ��ƃX�e�A������
���āA�R�[�i�����O�p���[���d�ɑ��Ĕ���`�������ꍇ�ɑO��d�ʔz���Ƃ̑g�ݍ��킹�ŃX�e�A�����ɗ^����e���ɂ��Đ������Ă��܂������A�T�X�y���V���������ɂ���ėႦ���E�ւ̉d�ړ����R���g���[�����邱�ƂłS�ւ̗։d���R���g���[�����A����ƃ^�C���̔���`���Ƃ̑g�ݍ��킹�ŐϋɓI�ɃX�e�A������ω�������Ƃ������Ƃ��\�ł��B�ȉ��ɂ��̗�Ƃ��č��E�d�ړ����^�C�������Ƃ̑g�ݍ��킹�ɂ����ăX�e�A�����ɗ^����e����������܂��傤�B
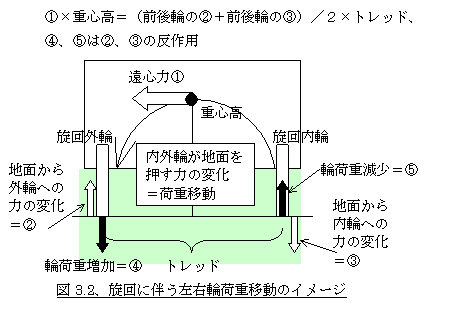
�@�܂��A���R�|�Q�A�d�ʔz���ƃX�e�A�����i�R�[�i�����O�p���[�̉d�ɑ������`��������ꍇ�j���ł̑O��d�ʔz���ƃ^�C������`�����Ƃ̑g�ݍ��킹�ɂ��X�e�A�����̐����ɂ����ẮA�b��P���ɂ��邽�߂ɑO��P�ւ��̂Q�փ��f���Ő������܂������A��������͍��E�֕ʁX�ɍl����K�v������܂��B�����Ȃ�Ǝԗ��d�S���Ɛ���ɔ������E�̉d�ړ��̉e�����o�Ă��܂��B�ԗ��̏d�S�����O�Ƃ������Ƃ͂��蓾�Ȃ��̂ŁA����Ήd������O���̎ԗւɂ̂�����������ԂɂȂ�A�O�ցi����O���̎ԗցj�̉d���傫���Ȃ�A���̕����ւ̉d���������Ȃ邱�Ɓi��������E�d�ړ����N��������ԂƂ����܂��j�͒����I�ɂ���������������Ǝv���܂��i�}3.2�Q�Ɓj�B���Ȃ݂ɂ��̂Ƃ��O��̊O�ւ̉d�����������ƁA�O��̓��ւ̉d�����������͓������Ȃ�܂��B�����łȂ��Ǝԏd������O�Ɛ��ŕω��������ƂɂȂ�A�w���N���X���N�����Ԃ������グ���艟�������肵�Ă��Ȃ����肻��Ȃ��Ƃ͂��蓾�Ȃ�����ł��B�i������R�ȓ����O��ŁA�ԗ��p���̕ω��ɂ���͓����̕ω��ȂǍׂ������Ƃ͂����ł͖����ł��B�j
��̓I�ȍ��E�d�ړ��ʂɂ��ẮA�}3.2���̋L�ڂ���
�@�~�d�S�����i�O��ւ̇A�{�O��ւ̇B�j�^�Q�~�g���b�h
�ԗ��d�ʁ~����G�~�d�S�����i�O��ւ̇A�{�O��ւ̇B�j�^�Q�~�g���b�h
�����ŁA�O��ւ̇A���O��ւ̇B�����ꂼ�ꂪ�O��փg�[�^���̍��E�d�ړ��ʂ̂��Ɓi�A�͊O�ւ����������A�B�͓��ւ����������j�Ȃ̂ŁA
�ԗ��d�ʁ~����G�~�d�S�����Q�~�u�O��փg�[�^���̍��E�d�ړ��ʁv�^�Q�~�g���b�h
�ƂȂ�A���������
�u�O��փg�[�^���̍��E�d�ړ��ʁv���ԗ��d�ʁ~����G�~�d�S���^�g���b�h
�ƂȂ�܂��B
�@���Ɋ֘A����̂͐���o�Ă����^�C���̔���`���ł��B�����ł��d�ɑ���R�[�i�����O�p���[�̔���`�����g���Đ������܂��B�ŏ��ɁA���̃^�C������`�����̗���`���Ă����܂��傤�B�����ł͗։d�Ƃ���ɑ���X���b�v�p�P���̂Ƃ��̃R�[�i�����O�t�H�[�X�i�R�[�i�����O�p���[�j�����Ɉȉ��̂悤���Ƃ��Ă����܂��傤�B
�\3.3�A�R�[�i�����O�p���[�̉d�ɑ������`���̗�Q
|
�։d |
�R�[�i�����O�p���[ |
|
|
�P�T�O������ |
�X�D�O�������^������ |
�։d�̂U�D�O�� |
|
�Q�O�O������ |
�P�P�D�O�������^������ |
�@�@�@�@�T�D�T�� |
|
�Q�T�O������ |
�P�Q�D�T�������^������ |
�@�@�@�@�T�D�O�� |
|
�R�O�O������ |
�P�R�D�T�������^������ |
�@�@�@�@�S�D�T�� |
|
�R�T�O������ |
�P�S�D�O�������^������ |
�@�@�@�@�S�D�O�� |
�v����ɐ���̗�Ɠ������։d���������Ă������ɂ̓R�[�i�����O�t�H�[�X�������Ȃ��^�C���Ƃ������Ƃł��B
�@�ԗ��͗�Ƃ��Ďԏd�P�O�O�O�������A�O��d�ʔz���͂T�O�F�T�O�̎ԂƂ��܂��B���Ȃ킿��葬���i���i���邢�͒�~���j�̂S�ւ̉d�͑S�ĂP�O�O�O�^�S���Q�T�O�������̎ԂƂ������Ƃł��B
�@�ŏ��ɍ��E�̉d�ړ����X�e�A�����ɂǂ̂悤�ɉe������̂��l���Ă݂܂��傤�B���܁A���̎Ԃ������������x�ł�����̔��a�̒��~���Ă���Ƃ��܂��B���E�̉d�ړ��������ꍇ�́A�e�։d�͂Q�T�O���������ł�����R�[�i�����O�t�H�[�X�͑O����ɃX���b�v�p�P��������P�Q�D�T�������Ƃ������ƂɂȂ�A���E�փg�[�^���ł͑O����ɃX���b�v�p�P��������Q�T���������Ƃ������ƂɂȂ�܂��B�O��ւ��������Ȃ���Ȃ�Ȃ��R�[�i�����O�t�H�[�X�������ŁA���O��ցi���E�g�[�^���j�̃R�[�i�����O�p���[�������Ȃ̂ŁA�O�փ^�C���X���b�v�p����փ^�C���X���b�v�p�ƂȂ�A���̎Ԃ̓j���[�g�����X�e�A�Ƃ������ƂɂȂ�܂��B�܂�A�O����ɓ����^�C�������ł���A���O��d�ʔz���̉e�����Ȃ��i�T�O�F�T�O�Ȃ̂Łj���Ƃ���A���̏ꍇ���̉e����������̎Ԃ̓j���[�g�����X�e�A���Ƃ������Ƃł��B
����A���̎Ԃ�����ɔ����O����ɍ��E�ɂT�O�����������E�d�ړ����Ă���ꍇ���l���Ă݂܂��B�܂�O�ւ͑O����ɂR�O�O�������ŁA���ւ͑O����ɂQ�O�O�������ł��B�O����ɊO�ւ��։d�R�O�O�������Ȃ̂ŃX���b�v�p�P��������P�R�D�T�������A�O����ɓ��ւ��։d�Q�O�O�������Ȃ̂ŃX���b�v�p�P��������P�P�������Ƃ������ƂɂȂ�A���E�փg�[�^������ƑO��ւƂ��ɃX���b�v�p�P��������Q�S�D�T�������ƂȂ�A���E�̉d�ړ��������ꍇ�ɔ�ׂĐ�Βl�͂O�D�T�������������Ă��܂����O��ւɍ����Ȃ����߂��̏ꍇ���ԗ��̓j���[�g�����X�e�A�ƂȂ�܂��B�i���������E�փg�[�^���ł̃R�[�i�����O�p���[���u�X���b�v�p�P��������̃R�[�i�����O�t�H�[�X�v�����E�d�ړ��̖����ꍇ�ɔ�ׂĂO�D�T�������������Ă���̂ŁA�������a�̉~���ԑ��i���Ȃ킿������������x�j�ŁA�����R�[�i�����O�t�H�[�X�Ő��邽�߂̃^�C���X���b�v�p��傫������K�v������A����������߂ɐ��Ă���Ƃ��̎ԑ̂̃X���b�v�p�͍��E�d�ړ��������ꍇ�ɔ�ׂđ傫���A���Ȃ킿���ΓI�ɂ������Ɍ������ƂɂȂ�܂��B�j
�ł͎��ɐ���Ɠ��������ŁA����ɔ������E�̉d�ړ��ʂ��O��ւňႤ�ꍇ�͂ǂ��Ȃ邩�l���Ă݂܂��傤�B�����ł͉��ɑO�ւ̍��E�d�ړ����P�O�O�������A��ւ��O�������Ƃ�����ōl���܂��傤�B���̏ꍇ������Ɠ��l�Ɏԗ��g�[�^���i�O��֍��v�j�ł̍��E�d�ړ��ʂ͂P�O�O�������ł��邱�Ƃ͕ς�肠��܂��A�O��ւ̕��S���Ⴄ�ꍇ�Ƃ����킯�ł��B
���Ă��̏ꍇ�A�O�O�ւ͗։d�R�T�O�������A�O���ւ͂P�T�O�������A��ւ͓��O���ɂQ�T�O�������ł��B���̂Ƃ��O�O�ւ̃X���b�v�p�P��������̃R�[�i�����O�t�H�[�X�͂P�S�������A�O���ւ͂X�������ŁA���E�փg�[�^���ł͂Q�R�������ƂȂ�܂��B��ւ͂��������O���ɂP�Q�D�T���������ł�����A���E�փg�[�^���łQ�T�������ɂȂ�܂��B���̏ꍇ�A�O�ւ͍��E�̉d�ړ��������ꍇ�ɔ�ׂăX���b�v�p�P��������̃R�[�i�����O�t�H�[�X���Q�T����������Q�R�������ɏ������Ȃ��Ă���킯�ł�����A���̕����������Ԃ�ۂ��߂ɗ]�v�Ƀ^�C���X���b�v�p���K�v�ɂȂ�܂��B�Ƃ��낪��ւ͍��E�d�ړ����Ȃ����߁A�O�Ɠ����X���b�v�p�P��������Q�T�������̃R�[�i�����O�t�H�[�X�����܂��B�]���Č�ւɕK�v�ȃ^�C���X���b�v�p�͐���̍��E�d�ړ��̂Ȃ��j���[�g�����X�e�A�̎ԂƓ����ŗǂ��A�]���Ďԑ̃X���b�v�p�������ł��B���̂��ߑO�ւ͖�W���]�v�ɕK�v�ɂȂ����^�C���X���b�v�p�邽�߁A�O�ֈʒu�ł̎ԑ̃X���b�v�p���ς��Ȃ��̂őO�֑NJp��]�v�ɐ�K�v������܂��B�v����ɂ��̎Ԃ̓A���_�[�X�e�A���Ƃ������Ƃł��B
���̗�ł͌�ւ̉d�ړ����O�Ƃ����ɒ[�ȏꍇ�ł����A�v����ɑO��ւō��E�̉d�ړ��̊������قȂ�Β萫�I�ɂ͓�������������킯�ł��B�O�ւ̍��E�d�ړ��̗ʂ���ւ̂�����傫����A����`�^�C�������Ƃ̑g�ݍ��킹�ŃA���_�[�X�e�A�̌X���������Ȃ�Ƃ������Ƃł��B
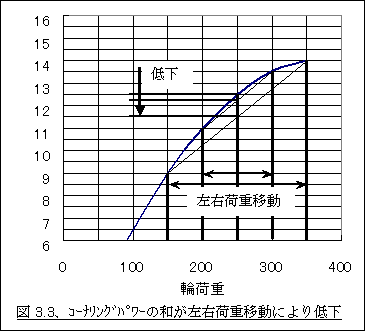
�ȏ�������Ă����̂́A�}3.3�Ɏ����悤�Ɂu�R�[�i�����O�p���[�ɉd�ˑ���������ꍇ�ɂ́A���E�d�ړ�����ƍ��E�փg�[�^���̗։d�͕ς��Ȃ��Ă��A���E�փg�[�^���̃R�[�i�����O�p���[�͉������Ă��܂��A���̉������͉d�ړ��ʂ��傫����Α傫���قǑ傫���v�Ƃ������ƁA�����Ă�������܂��R���g���[������X�e�A�����ɉe����^����Ƃ������Ƃł��B�܂�A�Ⴆ�Ώ����̏d�ʔz�����t�����g���ŃA���_�[�X�e�A�̎ԗ��̏ꍇ�ł��A����ɂ�鍶�E�̉d�ړ��ʂ���֑���傫�����邱�ƂŃj���[�g�����X�e�A�ɋ߂Â��邱�Ƃ��ł���킯�ł��B
 |
�����̍��ڂց��@�@���ڎ��ց��@�@���g�n�l�d�ց�