<8−2、具体的なサスペンションジオメトリとロールステア>
さて、ロールステアがステア特性など旋回性に与える影響の概念がわかったところで、今度は具体的にどのようなサスペンションジオメトリ(サスペンションの各パーツの寸法や構成・配置)でどのようなストローク〜トー角変化(ロールステア)を示すか、ごく簡単な例で説明しましょう。
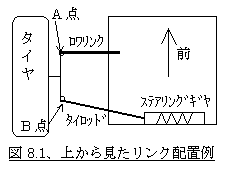
ここに平面図、図8.1のようなリンク配置のサスペンションがあったとします。この場合トー角は、ロワリンクの先端A点と、ステアリングギヤにつながるタイロッドの先端B点で形成されています。(実際のサスペンション構成にはこの他にストラットなどの上部リンクが必要ですがここではトー変化の説明のため省略しています)
このサスペンションを正面から見たときのリンク配置が仮に図8.2左のようになっていたとします。このサスペンションがバウンド側にストロークすると、ロワリンクの先端A点はリンクが外下がりに付いているためこの範囲では円弧に沿って外に振り出されますが、タイロッドの先端B点は中央付近ではほぼ垂直に上下し、さらにバウンドすると内側に入ってきます。このためバウンド側のトー角変化はある範囲まではA点が外に、B点が内に移動するため、バウンドトーアウトとなります(図8.2右参照)。尚、更にバウンドしてロワリンクが水平を過ぎるとA点は内側に入り始めるため、次第にトーアウト量は減ってきます。
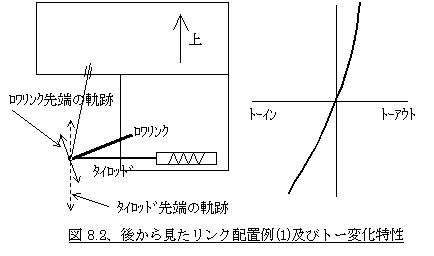 |
同じようにリバウンド側について考えると、A点もB点も内側へ移動しますが、ロワリンクの傾きの方がきついのと長さが短いことにより、A点の方がより内側に移動することになります。したがってリバウンド側のトー角変化はトーインということになるわけです。
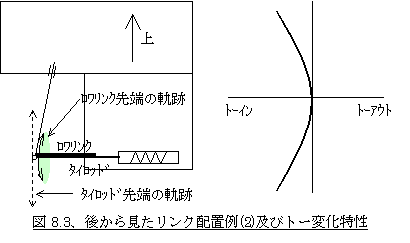
さて、図8.3左のようなリンク配置の場合はどうなるでしょうか。図のように中央位置でロワリンクもタイロッドも水平なので、バウンド側もリバウンド側も、A点、B点とも内側に入ることになります。但しこの例ではロワリンクの方がタイロッドより短いので円弧がきつく、同じストロークに対してより多く内側に移動します。したがってこの例ではバウンドもリバウンドもトーインということになるわけです(図8.3右参照)。
 |
以上は2本のリンクを考えればよい、非常に簡単な例ですが、どのように複雑なリンク配置のサスペンションにおいても基本は同じです。そのサスペンションのトー角を形成しているリンクそれぞれが、ストロークすることによってどのような軌跡を描くかを見極めることにより、ストロークに対するトー角変化を知ることができます。逆に、希望のトー角変化特性を得るためにどのようなリンク配置にすればよいかもわかるわけです。例えば図8.2のリンク配置例(1)で仮にバウンドトーアウト特性をもっと強くしたければ、ロワリンクの外下がりをもっときつくするとか、タイロッドを少し外上がりにするとか、ロワリンクの長さを短くするとかすればよいことがわかると思います。但し、サスペンションのジオメトリは、様々な要件を満たすため各種の特性を最適化する必要があります。したがって一つの特性から単純にジオメトリを決定することはできません。