<5-4、サスペンションジオメトリとジャッキアップ量>
ではこのジャッキアップ量はどのようにして決まるのか。今度は車体に入る入力の、上下方向の釣り合いをみてみましょう。図5.3は図5.2中の車体に入力される力(白矢印)を抜きだしたものです。
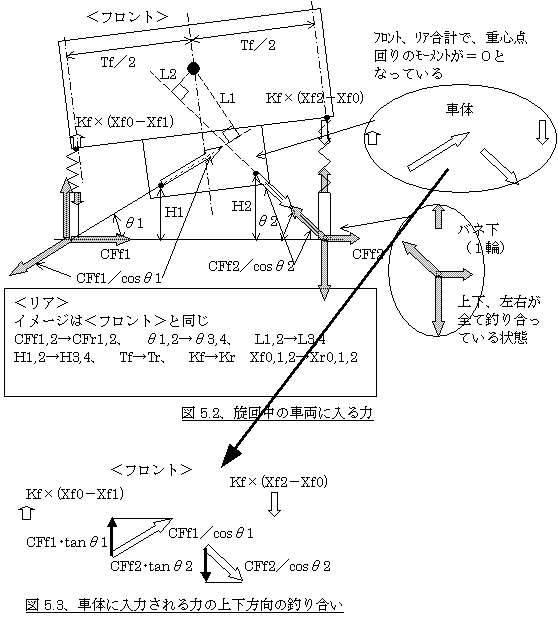
定常円旋回だから、車体はフロントもリアもどんどん上下方向に加速していかないわけだから、車体に入るフロント、リアそれぞれの上下方向の力は釣り合っている。したがって
①フロントの上下方向の釣り合い
CFf1×tanθ1-CFf2×tanθ2
+Kf×(Xf0-Xf1)-Kf×(Xf2-Xf0)
= 0
よって
CFf1×tanθ1-CFf2×tanθ2
= Kf×(Xf1+Xf2-2Xf0)
…(5-4)
②リアの上下方向の釣り合い
同様に
CFr1×tanθ3-CFr2×tanθ4
= Kr×(Xr1+Xr2-2Xr0)
…(5-5)
ここで、式(5-4)、式(5-5)の 赤字 と 青字 に着目すると、 赤字 は「ロールしている現状の左右ストロークの合計」であり、 青字 は「直進時の左右ストロークの合計」です。つまり式(5-4)の右辺がもし=0ならば、前輪のジャッキアップ量は0であり、もし+(プラス)であればジャッキアップ、もし-(マイナス)ならばジャッキダウンということになります。同様に、式(5-5)の右辺は後輪のジャッキアップ量を表しています。
つまりジャッキアップ量は
前輪:(CFf1×tanθ1-CFf2×tanθ2)/Kf
後輪:(CFr1×tanθ3-CFr2×tanθ4)/Kr
となるわけです。言い換えれば、ジャッキアップ量を0とするには、
前輪:CFf1×tanθ1-CFf2×tanθ2 = 0
後輪:CFr1×tanθ3-CFr2×tanθ4 = 0
となるようにサスペンションの瞬間回転中心(すなわちtanθ1~4)を設定すれば良いということになります。但し、旋回加速度が変わるにつれて内外輪のコーナリングフォースのバランスも変わるし、ロール角が変わるにつれて瞬間回転中心も刻々と変化していくので、全ての条件でこれを達成するようなサスペンションジオメトリは事実上不可能なのですが。
尚、念のため付け加えると、今までのことを踏まえればわかるように、ジャッキアップしているからといってその分輪荷重が抜けているわけではありません。仮にフロントがジャッキアップし、リアがジャッキダウンしていたとしても、別にそのこと自体で(前後重量配分のピッチ角による移動分は除き)フロントからリアに荷重移動しているわけではありません。同様にフロントもリアもジャッキアップしているからといって、前後輪の荷重がどこかに消えてしまうわけでもありません。あくまで力のやりとりにおいて内部のバネがより縮んだり伸びたりしているだけなのです。もう少し詳しくいえば輪荷重の左右移動量は増える量と減る量は等しいのですが、この移動量のうちバネで受け持たれるものと、サスペンションリンクで受け持たれるものがあること。そしてそれらがトータルで釣り合っているため、サスペンションリンクで受け持たれる上下力に左右アンバランスがある場合、それを是正するためにバネで受け持たれるものの量が左右輪で異なることになり、その結果、左右のストロークのアンバランスが生じて、ジャッキアップ・ジャッキダウンが発生するというわけです。
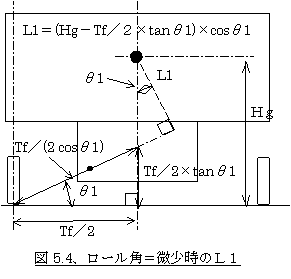 |
またいささか蛇足ですが、重心高をHg、ロール角を微少として無視すると図5.4の作図からL1は2つの三角形の相似から、
L1:Tf/2=(Hg-Tf/2×tanθ1):Tf/(2cosθ1)から
L1=(Hg-Tf/2×tanθ1)×cosθ1
=Hg・cosθ1-Tf/2×sinθ1
…(5-6)
同様に
L2=Hg・cosθ2-Tf/2×sinθ2 …(5-7)
L3=Hg・cosθ3-Tr/2×sinθ3 …(5-8)
L4=Hg・cosθ4-Tr/2×sinθ4 …(5-9)
式(5-6)~(5-9)を式(5-3)へ代入して整理すると
(CFf1+CFf2+CFr1+CFr2)・Hg
-CFf1・tanθ1・Tf/2-Kf×Tf/2×(Xf0-Xf1)
-CFf2・tanθ2・Tf/2-Kf×Tf/2×(Xf2-Xf0)
-CFr1・tanθ3・Tr/2-Kr×Tr/2×(Xr0-Xr1)
-CFr2・tanθ4・Tr/2-Kr×Tr/2×(Xr2-Xr0)
=0
…(5-10)
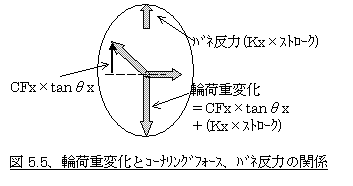
ここで図5.5からもわかるように、式(5-10)の下線部
CFf(r)x・tanθx・Tf(r)/2
±Kf(r)×Tf(r)/2×(Xf(r)x-Xf(r)0)
=ΔWf(r)・Tf(r)/2=「各輪荷重変化の合計×トレッドの半分」ことであり、重心点にかかる遠心力をYg×Wとすると
CFf1+CFf2=Wf×Yg、CFr1+CFr2=Wr×Ygから式(5-10)は
(Wf+Wr)・Yg・Hg-ΔWf・Tf-ΔWr・Tr=0 …(5-11)
 |
ここで<4-2、左右荷重移動におけるロールセンター高とロール剛性前後配分>の項を思い出していただくと、
Hg=ΔHg+Hf、もしくはHg=ΔHg+Hr
と考えれば、式(5-11)は
(Wf+Wr)・Yg・ΔHg+Wf・Yg・Hf+Wr・Yg・Hr
-ΔWf・Tf-ΔWr・Tr
=0
となり、<4-2、左右荷重移動におけるロールセンター高とロール剛性前後配分>の項の内容(式(4-1)に式(4-2)と(4-3)を代入したもの)と同じになります。