پƒ‚Tپ|‚RپA’èڈي‰~گù‰ٌ’†‚جƒچپ[ƒ‹ƒ‚پ[ƒپƒ“ƒg‚ج’ق‚èچ‡‚¢پ„
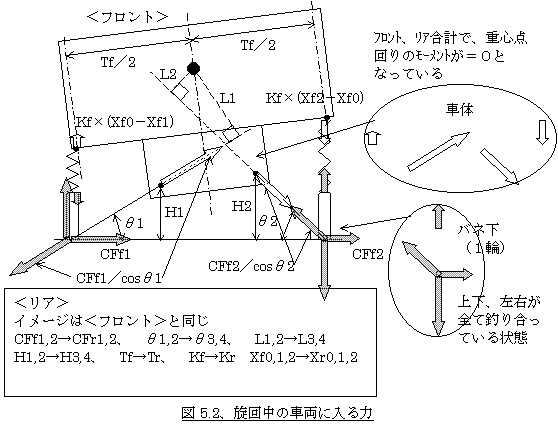
ڈuٹش‰ٌ“]’†گS‚جٹT”O‚ً—‰ً‚µ‚½‚ئ‚±‚ë‚إپA’èڈي‰~گù‰ٌژ‚جڈdگS“_‰ٌ‚è‚جƒ‚پ[ƒپƒ“ƒg‚ج’ق‚èچ‡‚¢‚ًچl‚¦‚ـ‚·‚ھپA‚±‚±‚إƒtƒچƒ“ƒgپEƒٹƒA‹y‚ر‚»‚جچ¶‰E‚»‚ꂼ‚ê‚ة‚آ‚¢‚ؤپA‚ي‚©‚è‚â‚·‚‚·‚邽‚كƒTƒXƒyƒ“ƒVƒ‡ƒ“‚حڈuٹش‰ٌ“]’†گS‚ًƒsƒ{ƒbƒg‚ئ‚·‚éƒٹƒ“ƒN‚P–{‚ة‰¼‘z‚µپA‚©‚آƒچپ[ƒ‹چ„گ«‚جŒ¹‚إ‚ ‚éƒoƒl‚âƒXƒ^ƒrƒ‰ƒCƒUپ[‚ئ‚µ‚ؤ‚حƒgƒŒƒbƒh‚جˆت’u‚ةژو‚è•t‚¯‚ç‚ꂽƒoƒl‚P–{‚إ‘م•\‚µ‚ؤچl‚¦‚邱‚ئ‚ئ‚µ‚ـ‚·پB‚ـ‚½پA’èڈي‰~گù‰ٌگù‰ٌ’†‚ةŒہ’肵‚ؤچl‚¦‚é‚ج‚إپAƒVƒ‡ƒbƒNƒAƒuƒ\پ[ƒoپ[•ھ‚ج—ح‚حچl‚¦‚ـ‚¹‚ٌپBگ}5.2‚ًژQچl‚ة‚µ‚ب‚ھ‚çˆب‰؛‚ً“ا‚ٌ‚إ‚‚¾‚³‚¢پB
 |
ژش—¼‚ھچ،’èڈي‰~گù‰ٌ‚µ‚ؤ‚¢‚é‚ئ‚µ‚ؤپA‚ـ‚¸ƒtƒچƒ“ƒg‚إژش‘ج‚ة“ü‚é—ح‚ًگô‚¢ڈo‚µپAڈdگS“_‰ٌ‚è‚جƒ‚پ[ƒپƒ“ƒg‚ًژZڈo‚µ‚ـ‚·پB”گ¶‚µ‚ؤ‚¢‚é—ح‚ئ‚µ‚ؤ‚حپA
‡@پFٹeƒ^ƒCƒ„‚ة”گ¶‚µ‚ؤ‚¢‚éƒRپ[ƒiƒٹƒ“ƒOƒtƒHپ[ƒXپi‰،Œü‚«پBچ¶‰E—ض‚إ‘ه‚«‚³‚ھˆظ‚ب‚é‚ج‚إƒtƒچƒ“ƒg‚جچ¶‰E‚ً‚»‚ꂼ‚ê‚ً‚b‚e‚†‚PپA‚b‚e‚†‚Q‚ئ‚µ‚ـ‚·پBƒRپ[ƒiƒٹƒ“ƒOƒtƒHپ[ƒX‚حکH–ت‚©‚çƒ^ƒCƒ„‚ة“ü‚é—ح‚إپAƒTƒXƒyƒ“ƒVƒ‡ƒ“ƒٹƒ“ƒN‚ً‰î‚µ‚ؤژش‘ج‚ة“ü—ح‚³‚ê‚ؤ‚¢‚ـ‚·پjپA
‡AپFƒoƒl”½—حپiƒoƒl‚©‚çژش‘ج‚ضپA‚ ‚é‚¢‚ح‚»‚ج”½—ح‚ھƒoƒl‚©‚çƒ^ƒCƒ„پiƒAƒNƒXƒ‹پj‚ضپBƒzƒCپ[ƒ‹’[ƒoƒl’èگ”‚ً‚j‚†‚ئ‚µƒoƒl‚ج’¼گiژ‚ج’·‚³‚ً‚w‚†‚OپAچ¶‰E—ض‚جƒoƒl‚ج’·‚³‚ً‚»‚ꂼ‚ê‚w‚†‚PپA‚w‚†‚Q‚ئ‚·‚é‚ئپAژش‘ج‚ة“ü‚éƒoƒl”½—ح‚ح‚»‚ꂼ‚ê‚j‚†پ~پi‚w‚†‚Oپ|‚w‚†‚PپjپA‚j‚†پ~پi‚w‚†‚Qپ|‚w‚†‚Oپj‚ئ‚ب‚è‚ـ‚·پBپj
ٹe‰¼‘zƒٹƒ“ƒN‚ج‰„’·گü‚ةڈdگS‚©‚炨‚낵‚½گ‚گü‚ج’·‚³‚ً‚k‚PپA‚k‚QپAƒٹƒ“ƒN‚ج’n–ت‚ئگ¬‚·ٹp‚ًƒئ‚PپAƒئ‚QپAƒgƒŒƒbƒh‚ً‚s‚†‚ئ‚·‚é‚ئ
‡@ژش‘ج‚ة“ü—ح‚³‚ê‚é—ح‚جڈdگS‰ٌ‚è‚جƒ‚پ[ƒپƒ“ƒgپiƒtƒچƒ“ƒg‰ٌ‚èپj
‚b‚e‚†‚Pپ~‚k‚Pپ^‚ƒ‚ڈ‚“ƒئ‚Pپ{‚b‚e‚†‚Qپ~‚k‚Qپ^‚ƒ‚ڈ‚“ƒئ‚Q
پ@پ|‚j‚†پ~پi‚w‚†‚Oپ|‚w‚†‚Pپjپ~‚s‚†پ^‚Qپ|‚j‚†پ~پi‚w‚†‚Qپ|‚w‚†‚Oپjپ~‚s‚†پ^‚Q
پi’A‚µپAƒچپ[ƒ‹‚ة”؛‚¤ڈdگS“_‚جچ¶‰Eˆع“®—ت‚ة‚آ‚¢‚ؤ‚ح‚±‚±‚إ‚ح–³ژ‹‚µ‚ـ‚·پj
‚و‚ء‚ؤ
‚b‚e‚†‚Pپ~‚k‚Pپ^‚ƒ‚ڈ‚“ƒئ‚Pپ{‚b‚e‚†‚Qپ~‚k‚Qپ^‚ƒ‚ڈ‚“ƒئ‚Q
پ@پ|‚j‚†پ~‚s‚†پ^‚Qپ~پi‚w‚†‚Qپ|‚w‚†‚Pپjپ@پ@پ@پ@پ@پ@پcپi‚Tپ|‚Pپj
پ@‡Aژش‘ج‚ة“ü—ح‚³‚ê‚é—ح‚جڈdگS‰ٌ‚è‚جƒ‚پ[ƒپƒ“ƒgپiƒٹƒA‰ٌ‚èپj
‚b‚e‚’‚Pپ~‚k‚Rپ^‚ƒ‚ڈ‚“ƒئ‚Rپ{‚b‚e‚’‚Qپ~‚k‚Sپ^‚ƒ‚ڈ‚“ƒئ‚S
پ@پ|‚j‚’پ~پi‚w‚’‚Oپ|‚w‚’‚Pپjپ~‚s‚’پ^‚Qپ|‚j‚’پ~پi‚w‚’‚Qپ|‚w‚’‚Oپjپ~‚s‚’پ^‚Q
‚و‚ء‚ؤ
‚b‚e‚’‚Pپ~‚k‚Rپ^‚ƒ‚ڈ‚“ƒئ‚Rپ{‚b‚e‚’‚Qپ~‚k‚Sپ^‚ƒ‚ڈ‚“ƒئ‚S
پ@پ@پ@پ|‚j‚’پ~‚s‚’پ^‚Qپ~پi‚w‚’‚Qپ|‚w‚’‚Pپjپ@پ@پ@پ@پ@پ@پcپi‚Tپ|‚Qپj
‚±‚±‚إ’èڈي‰~گù‰ٌ‚ئ‚¢‚¤ڈًŒڈ‚©‚çپAƒچپ[ƒ‹ٹp‰ء‘¬“xپپ‚OپA‚و‚ء‚ؤڈdگS“_‰ٌ‚è‚جƒgپ[ƒ^ƒ‹‚جƒچپ[ƒ‹ƒ‚پ[ƒپƒ“ƒgپپ‚OپB‚و‚ء‚ؤژ®پi‚Tپ|‚Pپjپ{ژ®پi‚Tپ|‚Qپjپپ‚O‚©‚ç
پ@پ@‚b‚e‚†‚Pپ~‚k‚Pپ^‚ƒ‚ڈ‚“ƒئ‚Pپ{‚b‚e‚†‚Qپ~‚k‚Qپ^‚ƒ‚ڈ‚“ƒئ‚Q
پ{‚b‚e‚’‚Pپ~‚k‚Rپ^‚ƒ‚ڈ‚“ƒئ‚Rپ{‚b‚e‚’‚Qپ~‚k‚Sپ^‚ƒ‚ڈ‚“ƒئ‚S
پ@پ|‚j‚†پ~‚s‚†پ^‚Qپ~پi‚w‚†‚Qپ|‚w‚†‚Pپjپ|‚j‚’پ~‚s‚’پ^‚Qپ~پi‚w‚’‚Qپ|‚w‚’‚Pپj
پ@پ@پپ‚O
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پcپi‚Tپ|‚Rپj
‚ئ‚ب‚è‚ـ‚·پB‚±‚ê‚حگ}5.2‚ج”’‚¢–îˆَ‚ج‚W‚آپi‘OŒم‚S‚آ‚¸‚آپj‚ج—ح‚ة‚و‚éڈdگS“_ژü‚è‚جƒ‚پ[ƒپƒ“ƒg‚ھƒ[ƒچپA‚·‚ب‚ي‚؟’ق‚èچ‡‚ء‚ؤ‚¢‚é‚ئ‚¢‚¤‚±‚ئ‚إ‚·پB
‚ئ‚±‚ë‚إگ}‚ًŒ©‚ê‚خ‚ي‚©‚é‚ئ‚¨‚èپAژ®پi‚Tپ|‚Rپj‚حچ¶‰E‚جƒRپ[ƒiƒٹƒ“ƒOƒtƒHپ[ƒX‚ھچ¶‰E‚جƒTƒXƒyƒ“ƒVƒ‡ƒ“ƒٹƒ“ƒNŒo—R‚إژش‘ج‚ة“ü‚é•ھ‚جƒ‚پ[ƒپƒ“ƒgپiژ®پi‚Tپ|‚Rپj’†پ@گشژڑپ@•”پj‚ًپAچ¶‰E‚جƒoƒl”½—ح‚جچ·‚ة‚و‚郂پ[ƒپƒ“ƒgپiƒچپ[ƒ‹چ„گ«‚ة‚و‚郂پ[ƒپƒ“ƒgپAژ®پi‚Tپ|‚Rپj’†پ@گآژڑپ@•”پj‚ھ‚¤‚؟ڈء‚µ‚ؤپA’èڈيڈَ‘شپiˆê’è‚جƒچپ[ƒ‹ٹpپj‚ئ‚ب‚ء‚ؤ‚¢‚邱‚ئ‚ھ‚ي‚©‚è‚ـ‚·پB
‚±‚±‚إڈd—v‚ب‚ج‚حپuچ¶‰E‚جƒoƒl”½—ح‚جچ·پvپپ‚j‚†پ~پi‚w‚†‚Qپ|‚w‚†‚PپjپA‚j‚’پ~پi‚w‚’‚Qپ|‚w‚’‚Pپj‚ح‚à‚؟‚ë‚ٌچ¶‰E‚جƒXƒgƒچپ[ƒN‚جچ·پi‚w‚†‚Qپ|‚w‚†‚PپjپAپi‚w‚’‚Qپ|‚w‚’‚Pپj‚ة‚و‚è”گ¶‚·‚é‚ي‚¯‚إ‚·‚ھپA‚±‚ج‚ئ‚«‚w‚†‚QپA‚w‚†‚P‚ـ‚½‚w‚’‚QپA‚w‚’‚P‚ح‚»‚ꂼ‚ê’¼گiژ‚ج’·‚³‚w‚†‚O‚ـ‚½‚ح‚w‚’‚O‚ة‘خ‚µ‚ؤپAگL‚ر—ت‚ئڈk‚ف—ت‚ھ“¯‚¶‚ئ‚حŒہ‚ç‚ب‚¢‚ئ‚¢‚¤‚±‚ئ‚إ‚·پB‚آ‚ـ‚èچإڈ‰‚ج’¼گiژ‚ج’·‚³‚ھ‰¼‚ة‚P‚O‚O‚چ‚چ‚¾‚ئ‚µ‚ؤ“à—ض‚ھ‚P‚Q‚T‚چ‚چ‚ةگL‚رپAٹO—ض‚ھ‚V‚T‚چ‚چ‚ةڈk‚ٌ‚¾‚ئ‚·‚é‚ئپi‚w‚†‚Qپ|‚w‚†‚Pپjپپ‚T‚O‚چ‚چ‚ئ‚ب‚é‚ھپA—ل‚¦‚خ‚±‚ê‚ھپA“à—ضپF‚P‚S‚O‚چ‚چپi‚S‚O‚چ‚چگL‚ر‚½پjپAٹO—ضپF‚X‚O‚چ‚چپi‚P‚O‚چ‚چڈk‚ٌ‚¾پj‚إ‚àپi‚w‚†‚Qپ|‚w‚†‚Pپjپپ‚T‚O‚چ‚چ‚ة‚ب‚èپA“¯‚¶پuچ¶‰E‚جƒoƒl”½—ح‚جچ·پv‚ھ“¾‚ç‚ê‚é‚ي‚¯‚إ‚·پB‚»‚µ‚ؤ‚±‚جڈêچ‡چ¶‰E—ض‚ج’†گS‚حپi‚S‚Oپ|‚P‚Oپjپ^‚Qپپ‚P‚T‚چ‚چژ‚؟ڈم‚ھ‚邱‚ئ‚ة‚ب‚è‚ـ‚·پB‚±‚ê‚ھƒWƒƒƒbƒLƒAƒbƒv‚إ‚·پB
پ@‚ئ‚ب‚é‚ئپA‚±‚جƒWƒƒƒbƒLƒAƒbƒv—ت‚حژ®پi‚Tپ|‚Rپj‚¾‚¯‚©‚ç‚إ‚ح‹پ‚ك‚ç‚ê‚ب‚¢‚ئ‚¢‚¤‚±‚ئ‚ة‚ب‚è‚ـ‚·پBژں‚جڈح‚إپAچ،“x‚حڈم‰؛•ûŒü‚ج’ق‚èچ‡‚¢‚ًچl‚¦‚邱‚ئ‚إپA‚±‚ê‚ً‹پ‚ك‚ؤ‚ف‚ـ‚µ‚ه‚¤پB