![]()
第1節 〈UFOは遠い宇宙から地球まで飛んで来れるのだろうか?〉
世界中でUFOを見た人や、写真に撮った人もたくさんいる。それらは、何か他の物と見間違えの可能性もあるだろう?また写真においても、UFOではなく何か別のものを撮ったか?あるいはトリック写真の可能性もあるだろう。仮にUFOが存在したとしても、それは、地球人の誰かが造って飛ばしているのかもしれない。
しかし、問題なのは、UFOが存在するか?しないか?ではなくて、何万光年あるいは何百万光年も離れた宇宙から飛んで来る事ができるのか?どうかである。
仮に、私たちの銀河系から比較的近い、アンドロメダ大星雲から地球まで飛んで来ているとすると、地球からアンドロメダ大星雲までの距離は230万光年(2.3×1019 km)であって、光の速度で飛んで来たとしても、230万年もかかってしまう。アインシュタインの特殊相対性理論によると、物体が光の速度に近づくにつれて、その物体の質量が重くなるため、どんな推進力を使っても、どんな莫大なエネルギーを使っても、光の速度は越えられないことになっている。
宇宙人がどれほど高度な科学技術を持っていたとしても、決して光の速度を越えて宇宙を飛ぶことはできないと考えられている。しかし、宇宙人は私たちより、“高度な科学技術を持っている”というだけではなく、科学の理論においてもはるかに進歩しており、私たち地球人の知らない数多くの理論を解明しているに違いない。その中には、タイム・スリップの理論、ワープの理論、重力コントロールさらなは、超能力にいたるまで存在しているに違いない。
もしそうなら、私たちが知っているごくわずかで、しかも不完全な科学の知識内で、例えば「宇宙はあまりにも広く、の星と星うを結ぶ距離があまりにも遠すぎる。その上アインシュタインの相対性理論により、光の速度は越えられない。」というだけの理由で、宇宙人がUFOに乗ってこの地球を訪れていることを否定することはできないだろう。
第2節 〈3次元空間ではないもう一つの空間〉
いかなる物体も光の速度は越えることができない。しかし、UFOはその230万光年の距離の内、ほとんどの距離を一瞬の内に移動してしまうと、聞いた事がある?もしこれが事実なら現代科学の理論において、矛盾したことが起きていることになる。UFOが遠く離れた宇宙から地球に飛んで来ていることが間違っていないとしたら、私たちが絶対に正しいと信じている科学理論の中で、何かが間違っていることになる。その科学理論とは、
①アインシュタインの特殊相対性理論(光の速度を越えることは不可能である。)
②宇宙の広がりは、現在観測されているだけの広がりを持った空間であり、その3次元的な距離も、宇宙全体の体積も、現在観測されている通りである。
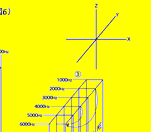
③この宇宙はX,Y,Z(縦、横、高さ)の方向に距離によって広げられた3次元空間である。
これら①,②,③の定義は世界中の人々が絶対に正しいと確信しているはずである。しかし、この3つの定義の中に一つだけ間違っている所がある。それは③の“この宇宙はX,Y,Z(縦、横、高さ)の方向に距離によって広げられた3次元空間である。”これは定義というより、誰一人疑う余地のない公理ともいうベき考え方であるが、実はこれが間違っている。
見かけ上は3次元空間と全く変わらないが、その空間のメカニズムが、X,Y,Z(縦、横、高さ)の方向に距離によって広げられた3次元空間とは全く異なったメカニズムでできた空間が考えられることが分った。そちらの空間では、3次元的に150億光年の広がりを持つ宇宙と比べて、その体積も密度も3次元的な距離も全く変らないばかりか、3次元的に移動した時の、周りの風景の移り変わる様子を見ても、3次元空間と全く変わらないように見えてしまう。
しかし、そちらの空間では、全宇宙の3次元的な広がりが、全て4次元的な広がりに移し替えられている。従って、今「3次元的な距離も全く変わらない。」と述べたが、正確には、3次元的な距離から、“見かけ上の3次元的な距離”に変換されていて、実際の3次元的な距離ではなくなっている。
そして、そちらの空間では、“見かけ上の3次元的な距離”が存在すると同時に、“次元を越えて移動した時の4次元的な距離”が存在していて、その4次元的な距離は全宇宙のどこと、どこを結んでも常に0(ゼロ)に保たれていることが分った。
光が見かけ上の3次元的な距離を何十億年もかけて届く距離であっても、UFOは次元を越えて4次元的に移動してしまうために、そこに距離は存在していない。そのため、UFOは一瞬の内に無限の距離を移動することができるのである。そこで、その空間のメカニズムについて考えてみることにする。
第3節 〈反物質でできた空間〉
それは、3次元的に広げられた空間を、全て4次元的な広がりに移し替えてしまえば完成してしまう。ここでは空間のメカニズム、つまり時間の流れを映画のフィルムの流れにたとえた時に、その連続的に入れ替っているフィルムの中の一コマに相当する一つの空間つまり、時間的に一つの周波数のエーテルでできた空間を取り出して考えてみる。
この宇宙の広がりを一辺が150億光年の距離を持った立方体とすると、その中には今仮に、時間としての周波数が全宇宙2000Hzのエーテルで満たされていたとする。しかし、エーテルの周波数はいくらでも掛け合わせることができる。そして、そのエーテルには、時間としての周波数と同時に空間としての周波数が存在している。
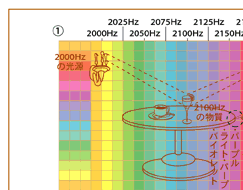
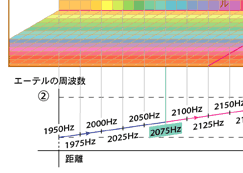
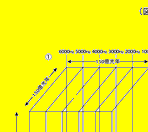
つまり、(図5) (1) ■ のように、150億光年の広がりを持った宇宙空間を、全てX,Y,Zの方向に、エーテルの周波数を連続的に変化させてしまう。もちろんエーテルの周波数を無限に細かく分けることはできないから、一つの軸、例えばX軸にいくつもの周波数を掛け合わせる。つまり、合成周波数にすることによって、150億光年の距離を全て周波数を変えてしまう。
図5-(1)~(3) |
||
 |
 |
|
 |
 |
同様にして、Y軸、Z軸も150億光年の距離を全て周波数を変えてしまう。そうすると、全宇宙を満たしたエーテルは、二点として同じ周波数の空間が存在しなくなり、全て周波数が違っていることになる。
そして、そのエーテルの中に存在している物質の周波数は(図5) (1) ■ のように、その物質が存在しているX,Y,Zの位置のエーテルの周波数と一致している。こうなってしまうと、自分の身の周りのエーテルの周波数は全て違っていることになり、そのエーテルの中に存在している物は、全て、立体映像のように、“硬さを持たない反物質”でできていることになってしまう。
もしそうなっているのだとすると、最初の『4次元の世界』の(図2) (1) ■ の所で述べたように、エーテルの周波数が違う空間(4次元)に存在している過去や未来は、“硬さを持たない反物質”となってしまい、光も物質も全て通り抜けてしまうために、目で見ることも、手で触れることも、できない。それに対して、自分の身の周りに存在している物は“硬さを持たない反物質”であるのに、自分の目ではっきり見ることができるし、手で触れることもできる。
その違いは、時間としてのエーテルの周波数の分け方は2000Hz、2001Hz、2002Hz、という具合に、その周波数と周波数の間が連続していなくて、その値が飛び飛びになっている。このような場合には(図2) (1) ■ のように、光も物質も全て通り抜けてしまう。
しかし(図5) (1) ■ のように、空間を満たしているエーテルは、その周波数が完全に連続していて、全くすき間なくつながっている。このような場合には、自分と周波数の違う光原から出た光でも、そのエーテルの中を進む間に、光の周波数が(図5) (1) ■ のように、そこのエーテルの周波数と同じ周波数になるように、周波数が変化しながら伝わるために、見えるのである。
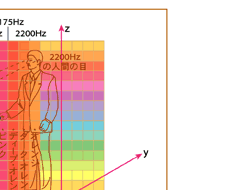
つまり、2000Hzの物質でできた光源から出た2000Hzの光が、2100Hzの物質に当たった時には、その光の周波数は2100Hzになっているため、その光はそこで反射し、そして、その光が2200Hzの人間の目にたちした時には、その光の周波数も2200Hzになっている。そのために、エーテルの周波数の違う所に存在している、周波数の違う反物質でも、見ることができるのである。
それでは、自分の身の周りに存在している物は全て自分と周波数が違っている、つまり“固さを持たない反物質”になっているはずなのに、どうして手で触れることができるのだろうか?それは、物質または人間が、連続的に周波数が変化したエーテルの中を移動すると、光と同様に、その物質の周波数が、そこの空間のエーテルの周波数と同じ周波数になるように変化してしまう。
そして(図5) (1) ■ の点線で囲んだ、男性の右手の指先と、丸いテーブルの右端が接する所のように、反物質と反物質が触れると、その反物質と反物質が接している所だけは、X,Y,Zの位置が一致している。従って、物と物が接する時は、どんな時でも必ず、X,Y,Z周波数が一致し同じ周波数のエーテルの中で接することになる。そのため、そこだけが物質化している。手をはなした瞬間にはもうその物体は、“固さを持たない反物質”に変化している。同様に、人間が自転車に乗って道路を走る時も、タイヤと道路が接する瞬間そこだけが物質化しているのである。
もし私たちの身の周りの空間がこのようなメカニズムでできているとすると、この世界は、自分の身の周りに存在している物質は自分の体と周波数が違っているため、全て立体映像のように、ただ見えているだけで、“堅さを持たない反物質”になっていることになる。
しかし、その反物質と反物質が接する所だけが物質化していれば、それでこの世界は成り立ってしまうのである。そのため、自分の身の周りに存在している物体は、全て反物質でできていることなど誰も気付かないに違いない。これは信じられないようなことだが、実際にそうなっている。
第4節 〈折りたたまれた空間〉
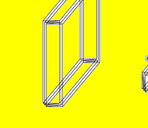
次に(図6) (1) ■ より、全宇宙の体積を一辺が150億光年の立方体とすると、この立方体をX軸において、全て等間隔になるように、宇宙の端から端までブロックに分けてしまう。
図6(拡大図あり) |
||
 |
 |
|
 |
 |
|
 |
 |
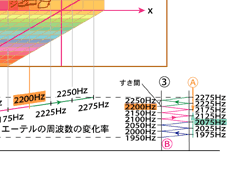
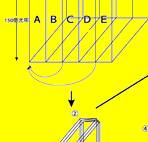
(図6) (1) ■ において、A,B,C,D,Eのそれぞれのブロックは、AからEの方向に連続的にエーテルの周波数が変化しているために、それぞれのブロックは全てエーテルの周波数が違っている。
エーテルの周波数の違う空間どうしは4次元的に重ねることができる。そこで、AのブロックにBのブロックを(図6) (2) ■ のように、ひっくり返して重ねてしまう。すると、CのブロックもBのブロックに引きづられて重なってしまう。
同様にAのブロックにDのブロックをひっくり返して重ねてしまうと、それに引きづられてEのブロックも重なってしまう。すると、(図6) (2) ■ のような一枚の厚手の板のような空間になってしまう。
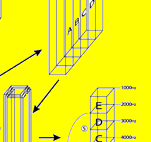
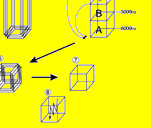
その一枚の厚手の板のようになった空間を、(図6) (3) ■ のように、Y軸において、X軸で分けたのと同じ間隔で全てブロックに分けてしまう。そして、Aのブロックに、Bのブロックをひっくり返して重ね、
さらにC,D,Eとそれぞれのブロックを、Aのブロックにひっくり返して重ねてしまう。すると、(図6) (4) ■ のような細長い柱のような形の空間になってしまう。さらに、その細長い柱のようになった空間を(図6) (5) ■ のように、X軸、Y軸で分けたのと同じ間隔で、全てブロックに分けてしまう。そして、AのブロックにBのブロックをひっくり返して重ね、さらにC,D,EとそれぞれのブロックをAのブロックにひっくり返して重ねてしまう。すると、(図6) (7) ■ のような小さな立方体のような空間になってしまう。(図6) (1) ■ のように、150億光年の3乗に広がった空間に満たされているエーテルを、X,Y,Zの三つの方向に周波数を変化させることによって、そのエーテルで満たされた空間を、X,Y,Zの三つの方向に、4次元的に折りたたむことができる。
(図6) (1) ■ では、一辺が150億光年の3乗に広がった空間が、X,Y,Zの方向にそれぞれ5等分されているが、それをもっと細かく分けることができる。
そこで、一辺が150億光年の距離をX,Y,Zの方向に150億等分して、全て重ねてしまうと、宇宙の3次元的な広がりは、一辺が1光年の3乗の立方体の空間に全て収まってしまう。
“1光年”というと、その数値は小さく聞こえるが、それをkmに直すと、およそ10兆kmとなり、まだまだ大きすぎる。そこで、さらに1億分の1に分けて重ねてしまうと、その大きさは、一辺が10万kmの立方体になってしまう。それでもまだ大きすぎるので、それをさらに1億分の1に分けて重ねてしまうと、一辺が1mの立方体になってしまう。それをさらに100の1に分けて重ねてしまうと、一辺が1cmの立方体になってしまう。
実際にはもっと小さく折りたたまれているはずだが、分りやすくするために、これぐらいの大きさで考えてみることにする。もともと150億光年の3乗の広がりがあった宇宙の体積が、4次元的に折りたたまれたために、一辺が1cmの3乗に広がった立方体の大きさになってしまったが、他の空間は、全て4次元的に重なり合った所に存在している。従って、体積は変化していない。
次に密度について考えてみると、4次元的に重なり合った立方体の中では、そのエーテルの周波数が(図5) (3) ■ ■ のようになり、連続せず、その値が飛び飛びになり、すき間ができてしまう。こうなってしまうと、(図2) (1) ■ のように、お互いに4次元的に重なり合った所に存在している周波数の違う物質は、全て反物質になってしまうため、どれだけ多くの物質が3次元的に共通の空間に存在していたとしても、周波数の違う物質は全て通り抜けてしまうため、密度も変わることがない。
また光も電波も音波も熱も4次元的に重なり合った、周波数の違うエーテルの間では伝わらない。従って、一つの空間に別の空間が、4次元的に重なり合って存在していることなど誰も気付かないに違いない。
それでは、4次元的に重なり合った所に存在している周波数の違う空間は、どこにも見ることができないのか?というと、決してそうではない。
(図7)(2) ■ から、この一枚の厚手の板のように折りたたまれ、4次元的に重なり合ったピンクのエーテルの空間に、自分がいたとする。そして、その4次元的に重なり合ったグリーンのエーテルの空間にある光源が存在していたとする。そして、その光源から光が放射されたとする。
すると、その光は(図7)(2) ■ の矢印のように4次元的に折りたたまれたエーテルの空間の左右の壁に当たるごとに反射し、次々と4次元的に折りたたまれた空間を一つ一つ通って、別の周波数の空間へと光がその周波数を変化させながら進み、自分がいる空間まで、何度も何度も、左右の壁の間を往復しながら伝わって来る。そして、私たちはその光を(図7)(1) ■ のように、自分の前方からまっすぐに、自分がいる方向に向かって来たものと、とらえてしまうため、(図7)(2) ■ のように、4次元的に重なり合った所に反物質の状態で存在している空間が、(図7)(1) ■ のように、全て自分がいる空間の外側に、3次元的に広がったところに存在しているかのように見えてしまう。
しかもこの空間は一つの方向ではなくて、三つの方向つまりX,Y,Zの方向に折りたたまれているとすれば、前後、左右、上下、斜めの、自分の身の周りに広がって見えている空間は、全て自分がいる空間の次元の違う空間、つまり4次元的に重なり合った所に存在している空間が、全て外側に広がった状態で見えていることになる。そのため、この宇宙は、1辺が150億光年の3乗の体積を持つ、折りたたまれる前の3次元空間のように見えてしまう。
しかし実際には、全宇宙の全ての空間は(図6)(6) ■ のように、3次元的に共通の空間に、エーテルの周波数を全て変えられて、反物質の状態で、4次元的に重なり合った所に存在している。これは信じがたいことだが、全宇宙の全ての空間は、私たちの体の外側に存在しているのではなくて、内側に存在しているのである。そして、私たちの体自体も、目に見えないくらい小さく折りたたまれているのである。
このようなメカニズムでできた空間を想像するには、(図7) (5) ■ のような立方体を作り、その内側に6枚の鏡をはり付ける。
図7-(5) |
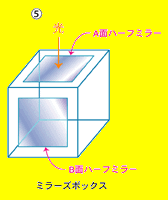 |
ただし、A面とB面は半分光が通り抜けるハーフミラーにする。そして、A面から光を入れ、B面からその立方体の中をのぞくと、一つの立方体が次々と周りの鏡に反射して、無限に広がった空間が見えるはずである。
その場合、周りに全て同じ一つの立方体が無数に映し出されて見えるが、見かけの位置に見えている立方体は、一つの立方体を除いて、全て虚像である。
4次元的に折りたたまれたエーテルの立方体の中を、光が反射しながら進んで行った場合には、3次元的に共通の空間に存在している、自分と周波数の違う物質や空間が、全て自分の身の周りに広がった状態で見えてしまう。
これは驚くべきことだが、私たちが見ているこの世界は、遠くに見えている物も、目の前に見えている物も、全て鏡に映し出されたような虚像を見ているのであって、見かけの位置には何も存在していないのである。
しかし、私たちの目に見えている虚像の方向に向かって進んで行こうとすると、(図7)(3) ■ のような小さな立方体の壁に当たるごとに、光が鏡に反射するように、進む方向が次々と変わり、4次元的に重なり合った所に存在している空間へと、少しづつ周波数が変化しながら進み、その物体が存在している(物質化している)次元にたどり着いてしまう。しかし、私たちにはエーテルが折りたたまれていることなど全く知らないから、(図7)(3) ■ のような小さな立方体の中での反射運動を、3次元的にまっすぐ移動しているように感じてしまうのである。
このように、4次元的に折りたたまれたエーテルの中での光もしくは物体の反射運動と、見かけ上の光もしくは物体の進む方向との関係を理解しやすくするために、(図8) (1),(図8) (2),(図9) (1), (2), (3)から考えてみることにする。
光が鏡に当たった時に、その光が実際に進む方向と、見かけ上の方向とではどのような違いがあるだろうか?(図8) (1) ■ において、Aの方向から来た光が、B点で30度の角度で鏡に当たると、B-Cを軸とした線対称の方向に、入射角と同じ30度の角度で反射し、反対方向のDの方向に進む。
同様に、Fの方向から来た光が、B点で60度の角度で鏡に当たると、それと反対方向に入射角と同じ60度の角度で反射し、Gの方向に進む。このように、光が鏡に対してどんな角度で当たっても、入射角と同じ角度で反射し、反対方向に進む。
それでは光の進む見かけ上の方向はどうだろうか?AからBの方向に鏡面に対して30度の角度で進んで来た光をDの位置から見ると、B点で鏡を突き抜けて、D-Bの直線をそのまままっすぐ延長したEの方向から進んで来るように見えるはずである。同様に、FからBの方向に鏡面に対して60度の角度で進んで来た光をGの位置から見ると、B点で鏡を突き抜けて、G-Bの直線をそのまままっすぐ延長したHの方向から進んで来るように見えるはずで
ある。
このことから分るように、“光が鏡面に対して何度の角度で当っても、その光の進む見かけ上の方向は、その鏡を突き抜け、その光をまっすぐ延長した方向に進むように見える。”これを(定義)(1)とする。
複数の鏡に光が連続的に当たった時に、その光が実際に進む方向と、見かけ上の方向とではどのような違いがあるだろうか?このことを(図8) (2) ■ の潜望鏡を用いて考えてみることにする。
(図8) (2) ■ において、Aの方向から入って来た光が実際に進む方向は、B,C,D,Eの鏡に次々と反射し、A,B,C,D,E,Fの点を結んだ線の方向になる。
それでは、見かけの位置はどのように見えるだろうか?まずAから入って来た光を“aの位置”で見ると、A点は“Bの鏡”の向う側のA′点に見えるはずである。
次に“bの位置”から見ると、A点、B点は“Cの鏡”の向う側のA″点、B′点に見えるはずである。
次に“Cの位置”から見ると、A点、B点、C点は“Dの鏡”の向う側のA"'点、B″点、C′点に見えるはずである。
そして、最後に“dの位置”から見ると、A点、B点、C点、D点は“Eの鏡”の向う側のA""点、B"'点、C"点、D'点に見えるはずである。
このことから分かるように、潜望鏡ののぞき穴“dの位置”から見ると、その潜望鏡の中に何枚の鏡があって、光が何度反射しても、その見かけの位置は、F-Eの直線を“Eの鏡”(最初の鏡)の裏側にまっすぐに延長した直線方向に、全て虚像として見えるはずである。
このことから“光が何度鏡に反射しても、見かけ上の位置は、光が(最初の鏡)に当った、その入射角を、そのまままっすぐ延長した方向に見える。”これを(定義)(2)とする。
一つの立方体の中での3次元的な反射運動は、(図7) (3) ■ のような3次元的な反射運動になるが、ここでは (図7) (3) ■ の立方体の上の面と下の面の反射運動は考えず、周りの4面の反射運動についてのみ考えてみることにする。
まず(図9) (1) ■ の一番下の白い正方形において、その周りの4面に鏡がはり付けられていたとする。そして、その中のA点から光が出たとする。すると、その光は、周りのA,B,C,Dの鏡に次々と反射し、白い小さな正方形の中の、実線の失印のような反射運動をすることになる。
それでは、光の進む見かけ上の方向は、どのように見えるのだろうか?それは、先ほどの(定義)(1)の“光が鏡面に対して何度の角度で当っても、その光の進む見かけ上の方向は、その鏡を突き抜け、その光をまっすぐ延長した方向に進むように見える。”と、(定義)(2)の“光が何度鏡に反射しても、見かけ上の位置は、光が(最初の鏡)に当ったその入射角を、そのまままっすぐ延長した方向に見える。”から、(図9) (1) ■ のA点かう出た光は、最初に当たったAの鏡を突き抜け、その光をまっすぐ延長した、点線の矢印の方向に進んで行くように見えるはずである。
そして、このことは(図9) (2) ■ の中心の、周りの四つの壁を鏡で囲まれた、白い小さな正方形の枠の中の光原から、周り360度のどの方向に向かって出た光も、周りの鏡に次々と反射し続け、決してその白い小さな正方形の枠の外に出ることはない。
しかし、それらの光の進む見かけ上の方向は、それらの光が一番最初の鏡に当たった時の入射角を、そのまままっすぐ延長した方向に進んて行くように見えるため、この白い小さな正方形の枠の外側に、(図9) (2) ■ のように、2次元的に広がった平面が写し出されて見えるはずである。
ここまでは、上下の反射運動を考えず、2次元的に考えて来たが、この白い小さな正方形の枠の上と下にも鏡をはり付け、上下方向の反射運動を加えたとしても同じことで、内側の壁6枚全てを鏡で囲まれた立方体(ミラーズ・ボックス)の中から出た光は決して、その立方体の外に出ることはないが、その光の進む見かけ上の方向は(図9) (3) ■ のように、この立方体(ミラーズ・ボックス)の外側に、3次元的に広がって行くように見えるため、そこに、3次元的に広がった空間が、写し出されて見えるはずである。そして、この“ミラーズ・ボックス”の考え方は、そのまま4次元的に折りたたまれたエーテルに置き替えることができる。
4次元的に折りたたまれたエーテルの中では、光、電波、音波、熱、重力波、運動エネルギー(慣性の法則)などのあらゆる波動が、ミラーズ・ボックスの中で、光が反射運動するのと全く同じように伝わることになる。従って、その中に入ってしまうと、4次元的に折りたたまれたエーテルが、全て外側に広がった状態で見えてしまう。そのため、3次元空間と全く変わらないように見えてしまうはずである。
このようなメカニズムで広げられた空間の中では、3次元的な運動は、全て3次元的な反射運動に置き替えられてしまうため、その小さな立方体の壁を越えて、まっすぐに移動することは不可能である。しかし、その小さな立方体の中にいる私たちは、3次元的な反射運動を、全て3次元的な直進運動として見えてしまう。従って、見かけ上3次元的にどんなに遠くまで移動したつもりでも、常に同じ一つの小さな立方体の中にいるのである。
しかも、その一つの単位となる立方体の大きさは、私たちの目にも見えないくらい小さいに違いない。とすると、私たちの体自体も小さく折りたたまれていて、私たちはその小さな立方体の中を反射運動しているどころか、わずかに振動しているにすぎないのである。
どうしてこのようなメカニズムにしてしまう必要があるのだろうか?それは、この空間のメカニズムこそが“ワープ”つまり、間の空間を全く通らずに、どこへでも、またどんなに遠く離れた所へでも、一瞬の内に移動することを可能にする唯一の空間のメカニズムだからである。
この4次元的に折りたたまれたエーテルに従って、光、電波、音波、熱、重力波、運動エネルギー(慣性の法則)などのあらゆる波動が伝わるとすると、その折りたたまれたエーテルの中に入ってしまうと、エーテルが折りたたまれていることなど決して分らないはずであり、エーテルがどんなに小さく折りたたまれていたとしても、まっすぐにX,Y,Zの方向に広がった3次元空間のように見えてしまうはずである。ところが、この宇宙の中でただ一つだけ次元を越えて移動することができる物がある。それがUFO(unidentified flying object)である。トリック写真参照
飛行機やスペースシャトルが3次元空間を移動する場合、見かけ上は(図7) (1) ■ のように、直線的に移動しているように見えるが、実際には(図7) (2) ■ のように、エーテルが4次元的に折りたたまれているために、小さな空間を反射運動しながら、その物体の周波数がその空間のエーテルの周波数と一致するように、絶えず周波数変換をしているのである。
(図7) (2) ■ は分りやすくするために、X軸だけを折りたたんだ図である)X,Y,Zの3つの方向にエーテルを折りたたむと、小さな立方体のような空間になってしまい、その中では、直線的な移動であっても、(図7) (3) ■ のような3次元的な反射運動になってしまう。
このことを理解しやすくするために、一つ次元を下げて考えてみることにする。
私たちが生きている、見かけ上3次元的に広がったように見えているこの宇宙を、一つ次元を下げて、2次元的な広がりにしたのが(図10) (1) ■ である。
2次元の平面でできた宇宙の中に、高さという方向を全く知らない人類がいたとする。その2次元の宇宙は1枚の紙の上に存在していて、その紙にそって光、電波、音波、熱、重力波、運動エネルギー(慣性の法則)などのあらゆる波動が伝わるようにできているとする。
そして、その紙の上に絵や図形が描かれているが、2次元の世界の人類にとっては、絵や図形を3次元的に重ねることも、面に面を重ねる(紙の上に紙を3次元的に重ねる)ことも不可能だと思っているし、またXとYの二つの軸によって特定できる場所は一つしかないと思っている。
ところが、その紙は(図10) (2) ■ のようにX軸で折りたたまれ、さらに(図10) (3) ■ のようにY軸で折りたたまれているため、2次元的な広がりが、一つの単位となる正方形を除いて、全て3次元的な広がりに移し替えられている。従って、(図10) (4) ■ のように、見かけの位置に見えている物は全て虚像であって、そんな所には何も存在していない。
しかし、その虚像が見える方向に向かって、まっすぐに進んで行こうとすると、見かけの方向が次々と変わるが、それを直線と感じながら、一つの正方形の中を(図10) (5) ■ のような反射運動をすると同時に、少しづつ高さを変えながら進み、目的地にたどり着いてしまう。後ろを振り返ると、光も自分が進んで来たのと同じように進むため、直線上にスタート地点が見える。
その3次元的に折りたたまれた紙の中に住んでいる人類にとっては、(図10) (5) ■ を直線と感じ、それが最短距離だと思っているし、そこを通らずに移動することは不可能だと思っている。
しかし、UFOはその3次元的に折りたたまれた面に対して、(図10) (4) ■ のように、高さ方向Z方向)に“次元を越えて3次元的に”移動してしまう。すると、高さという方向を知らない人類にとっては、どのように見えるだろうか?全ての面は3次元的に重なっているために、ほんの少し高さ方向(Z方向)に移動しただけで、(図10) (5) ■ のように、正方形の中を反射運動することなく、(図10) (1) ■ のAの位置からBの位置へ、間の面を全く通らずに瞬間移動したように見えるはずである。
このように、2次元的に広がった紙をXとYの二つの方向に折りたたんで、2次元的な広がりを全て3次元的な広がりに移し替えてしまっても、光、電波、音波、熱、重力波、運動エネルギー(慣性の法則)などのあらゆる波動が、折りたたまれた紙に従って伝わるとすれば、その折りたたまれた紙の中に入ってしまえば、全て折りたたまれる前の2次元的に広がった平面として見えてしまう。その中を高さ方向(Z方向)に“次元を越えて3次元的に”移動してしまえば、その紙の上のどの位置からどの位置へでも、間の面を全く通ることなく2次元的にワープすることが可能になってしまう。
私たちが生きているこの宇宙は、見かけ上3次元的に広がった空間のように見えているが、実際には、その3次元的な広がりが全て4次元的な広がりに移し替えられている。そのため、UFOは“次元を越えて4次元的に”移動することで、3次元的にワープすることができるのである。
この3次元的なワープの理論は、今まで述べて来た2次元的なワープの理論を、一つ次元を高めて考えれば容易に理解できるはずである。それは2次元の世界の紙に相当するのが、3次元の世界ではエーテルに当たり、2次元の紙は、XとYの二つの方向に高さを少しづつずらすことで、3次元的に折りたたんでしまうことができる。
すると、2次元的な広がりが、その面積を変えることなく、一つの単位となる正方形を除いて、全て3次元的な広がりに変わってしまう。そのため、UFOは“次元を越えて3次元的に”移動することで、2次元的にワープすることができるのである。
3次元空間に満たされたエーテルは、X,Y,Zの三つの方向に連続的に周波数を変えてしまうことで、三つの方向に4次元的に折りたたんでしまうことができる。すると、3次元的な広がりが、その体積を変えることなく、一つの単位となる立方体を除いて、全て4次元的な広がりに変わってしまう。
2次元の紙の上に描かれた絵や図形は、その紙と同じ高さに描かれている。その絵や図形に相当するのが、3次元の世界では物質に当り、その物質の周波数はその位置のエーテルの周波数と一致している。その物質が移動しようとすると、一つの単位となる立方体の中を(図7) (3) ■ のような3次元的な反射運動をしながら、少しづつ周波数が変化することで、目的の次元にたどり着いてしまう。
このように、4次元的に折りたたまれたエーテルのどの周波数の空間の中にいても、そこから周りに広がって見えている空間及びそこに見えている物質は全て虚像であって、見かけの位置には何も存在していない。目に見えている物が実際に存在している所は、自分の体と完全に重なり合った空間(4次元)に、全て反物質の状態で存在している。
見かけ上X,Yの方向にまっすぐに広がった2次元の世界に住んでいると思っている人類にとって、未知の方向である高さを“次元を越えて3次元的に”移動すれば、間の面を全く通ることなく、2次元的なワープができるように、見かけ上X,Y,Zの方向にまっすぐに広がった3次元の世界に住んでいると思っている人類にとって、未知の方向である4次元の方向に“次元を越えて4次元的に”移動すれば(自ら周波数を変えてしまえば)、間の空間を全く通ることなく、3次元的にワープしてしまう。それでは、自ら周波数を変えるためにはどうすればいいのだろうか?
空間に満たされたエーテルは(図5) (1) ■ のように、X,Y,Zの三つの方向にその周波数が連続的に変化しているため、全宇宙のどこの空間のエーテルも全てX,Y,Zの合成周波数によってできている。従って、今自分が唯一次元を越えて移動することができる乗り物であるUFOに乗っていたとすると、そのUFOの周波数を、目的の次元の三つの合成されたエーテルの周波数と一致させるように、三つの周波数を自ら変えてしまえば、3次元的にどんなに遠く離れた所であっても(何十億光年離れていても)、一瞬の内にワープしてしまうはずである。
それでは、UFOの周波数はどうすれば変えてしまうことができるのだろうか?それは、テスラコイル(図19) (1) ■ 、(図24) (2) ■ を使ってUFOに磁力線を送り込み、強力な磁場を発生させ、その磁場によってUFOを包み込んでしまう。すると、一瞬の内にUFOの周波数が変わってしまう。
3次元的なワープを可能にするためには、三つのテスラコイル(図19) (1) ■ 、(図24) (2) ■ が必要で、その三つのテスラコイルは、(図7) (4) ■ UFOの下に三つの丸い物が付いているが、その中入っている。そして、その三つのテスラコイルを使って、目的地のエーテルの周波数と一致するように磁力線を発生させ、その磁力線による磁場でUFOを包み込んでしまう。すると、UFOはそのUFOを構成している物質の周波数が、一瞬の内に変化し、“次元を越えて4次元的に”移動してしまう。これによって、UFOは、この宇宙のどことどこを結んでも、間の空間を全く通ることなく、3次元的にワープすることができる。これが3次元的なワープを可能にする理論である。(トリック写真参照)
| このホームページはダイジェスト版のため、本文の1部をカットしています。 |
フィラデルフィア実験の時も軍艦エルドリッジ号対して同じことが行われた。その結果エルドリッジ号の周波数変化し、テレポート=ワープしたと考えられる。
![]()