|
加速する質量から放出されるエネルギーを計算する公式
加速する質量から放出されるエネルギーを計算する公式を作りました。 これが加速する質量から放出されるエネルギーを計算する公式です。 [1] 
Eはエネルギー、tは時間、Gは万有引力定数、mは質量、aは加速度、cは光速です。 この公式は、加速する電荷から放出されるエネルギーの公式を元に作りました。 次の式が加速する電荷から放出されるエネルギーを計算する公式です。 [2] 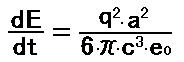
Eはエネルギー、tは時間、qは電荷、aは加速度、cは光速、e0は真空の誘電率です。 この公式は、量子力学の入門書によく出てきます。 古典力学で水素原子の周りの電子の回転を計算すると、電子は電磁波を放出しながら短時間で原子核に衝突するという思考実験で使われます。 この式を次のように書き直します。 [3] 
[3]の右の部分は、下記のように2つの部分に分かれています。 左の部分は、加速度と光の速度で構成されていて、右の部分は、電荷で構成されています。 このことから、次のことが推測されます。 距離の二乗で減衰するエネルギーの形態を持ち、そのエネルギーの伝わる速度が光速ならば、どのようなエネルギーにでも使えるのではないかということです。 その仮説を元に、電磁力の式を重力の式に置き換えてみます。 [4] 
[4]の右の部分は、次のように書き換えることが出来ます。 [5] 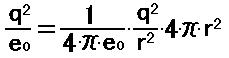
[5]の右の部分を二つに分けると、左はクーロン力、右は球の表面積になります。 [6] 
[5]のクーロン力を重力に置き換え 、球の表面積をかけると、次の式になります。 [7] 
この式を[3]に代入すると、次の式になります。 [8] 
この式が、加速する質量から放出されるエネルギーを計算する公式です。 さらに詳しく検証します。 この公式は元々は電磁力の公式なので、公式を導く手順を、電磁力と重力を対比しながら説明します。 次の図は、円の中心の電荷が右方向に加速した状態(加速度は a )を図にしています。 ただし、電荷の加速による移動速度は光速に比べて、かなり遅い場合です。 電荷が中心にあるときは、電荷は静止していて、電場は光速で球殻状に広がります。 中心から放射した電場は、T + t の時間で外円に到達します。 加速度 a で電荷が加速して、速度が v になった瞬間、t だけ遅れて放射した電場は時間 T で内円に到達します。 加速後に放射した電場は、中心から放射した電場よりも下の位置に到達します。 図では、2本の電場が描かれていますが、実際には連続した1本の電場です。 ct の幅で電場の向きを見ると、下の電場は上の電場の方向を向いています。 ようするに、一本の電場が傾いているのです。 つまり、電荷が静止している場合は、電荷の中心から放射状の電場しか存在しませんが、電荷が加速すると円の表面と平行な成分が出現します。 図では、折れ曲がった電場を E 、それを球の中心方向の電場 ER と球の表面と平行な成分 ET で表しています。 T は、電場が内円に到達する時間で、かつ電荷が図の右の位置に移動する時間。 ( T + t )は、電場が外円に到達する時間。 v と t は、v=at の関係(a は加速度)。 [9] 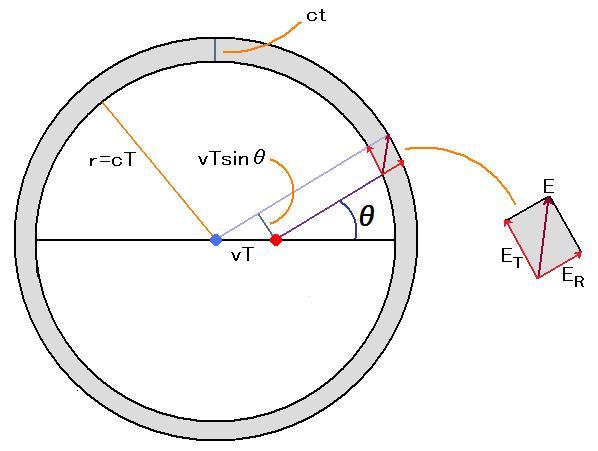
まずは、電荷がエネルギー放射する仕組みを説明します。 図から分かるように ER とET の比は次式になります。 [10] 
加速度は a=v/t の関係から[10]は次式になります。 [11] 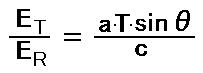
ERに関してはクーロンの法則により、次式で表すことが出来ます。 [12] 
[11]に[12]を代入して整理すると、次式になります。 [13] 
電場を二乗して真空の誘電率をかけると、圧力になります(単位はパスカル)。 [14] 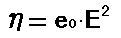
[14]に[13]を代入すると、次式になります。 [15] 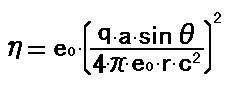
この式を球殻状に積分すると、放出エネルギーになりますが、次の図のようにETの大きさは球に対して対象性があるので、積分が簡単になります。 ETは、電荷の加速と垂直の方向が最大になり、平行の方向が最小になります。 平面では π/2 の位置がETの大きさの平均になりますが、実際には球ですので、この図を3次元のデカルト座標に移して計算します。 電荷がx軸上を動くことにすると、ETの大きさの平均は、x=y=z の位置になります。 三角関数の関係式を使うと、[17]になります。 [16] 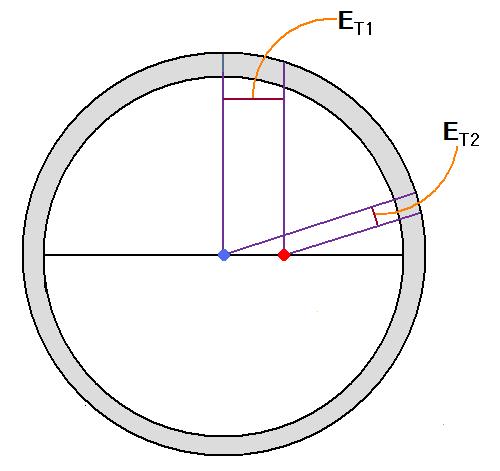
[17] 
[15]に[17]を代入して、球殻の体積(4πr^2×ct)をかけると、エネルギーと仕事率は次式になります。 仕事率の式が、加速する電荷から放出されるエネルギーの公式です。 [18] 
次に、電荷がエネルギーを放射する仕組みを、質量がエネルギーを放射する仕組みに置き換えて説明します。 電磁力を重力に対応させるためには、電荷を質量に、電場を重力加速度に対応させます。 [10]に対応する重力の式は、次式になります。 [19] 
[19]は、v=at の関係から、次式になります。 [20] 
[12]に対応する重力の式は、次式になります。 G は万有引力定数です。 [21] 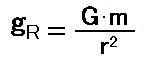
[20]に[21]を代入すると、次式になります。 [22] 
さらに r=cT の関係から、次式になります。 [23] 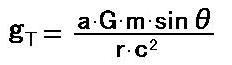
ここで、電荷と質量の力の関係を調べます。 2つの同じ電荷、2つの同じ質量に働く力は、次式です。 [24] 
電場と重力加速度を並べて書くと、次式になります。 [25] 
[25]を変形して電荷と質量を並べて書くと、次式になります。 [26] 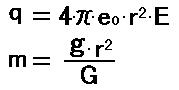
この式を[24]に代入すると、次式になります。 [27] 
この式を圧力の単位にするために 4πr^2 で割ります。 4kπe0=1 になるので、結局[14]の圧力の式になります。 [28] 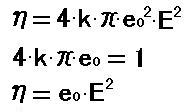
同じように[27]の重力の式も圧力の単位にするために 4πr^2 で割ると、次式になります。 [29] 
この式に[23]を代入すると、次式になります。 [30] 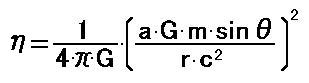
[17]で計算した sin^2θ=2/3 を[30]に代入すると、次式になります。 [31] 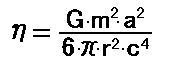
この式に球殻の体積をかけると、エネルギーの式になります。 [32] 
この式を時間で割ると、単位時間あたりのエネルギーを放出する式になります。 この式は、[1]と同じ式です。 [33] 
重力の放射エネルギーの式にたどり着くために、数式の形式的な置き換えに終始しましたので、中身が分かりにくかったと思います。 ここでは、上記に出てきた、式[29]の実態は何かを考えてみます。 [29] 
式[29]に対応する電荷の圧力は、1/2をかけることで静電エネルギーの密度になります。 [34] 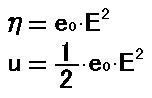
そこで、電荷の圧力と静電エネルギーの関係を真似て、重力の圧力の式[29]に1/2をかけると静止重力のエネルギーの密度の式になるという仮説を立てます。 [35] 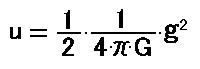
ある質量が静止重力エネルギーを持つとすれば、その値は、質量を取り巻く全空間に対して、静止重力エネルギー密度を積分すれば求められます。 では、実際に地球に対してこの計算を行ってみます。 計算は、地球の外部と地球の内部に分けて行い、後で合計します。 地球の半径を a とします。 地球の外部の静止重力エネルギーを計算します。 [36] 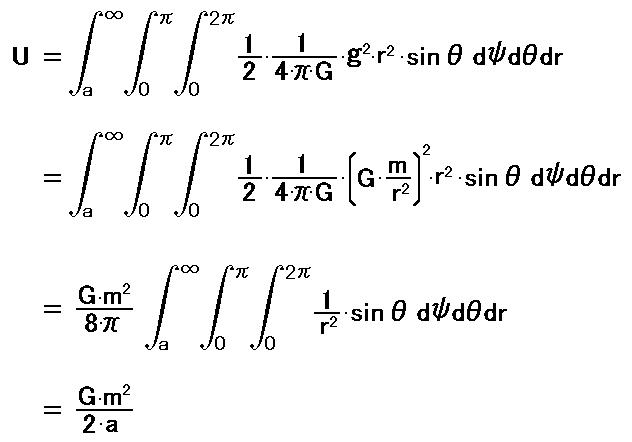
地球の内部の静止重力エネルギーを計算します。 地球の密度は一定とします。 [37] 
地球の外部と内部の静止重力エネルギーを合計すると、全静止重力エネルギーになります。 [38] 
この式に実際の値を代入して地球の全静止重力エネルギーを求めてみます。 [39] 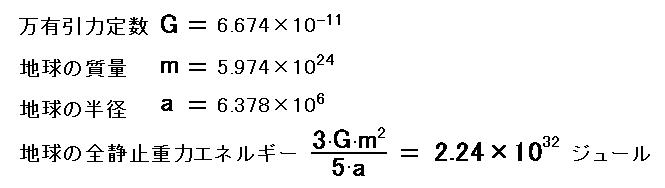
地球の全静止重力エネルギーは、地球を小さな破片に分解して、無限遠方に運んで行くのに必要なエネルギーと同じはずです。 この計算をプログラムを使って行います。
double GA, HANKEI, OMOSA, US, PAI, MITUDO;
double m1, m2, w1, w2, r1, hb, x, g;
int ct1;
PAI = 3.14159;
GA = 6.674 * pow(10,-11); //万有引力定数
US = 5000000000; //重力の影響があまりない地点(無限遠方のつもり)と地表との距離(メートル)
HANKEI = 6.378 * pow(10,6); //地球の半径(メートル)
OMOSA = 5.974 * pow(10,24); //地球の質量(キログラム)
MITUDO = OMOSA / ((4.0 / 3) * PAI * pow(HANKEI,3));
m1 = OMOSA;
m2 = 1 * pow(10,22); //移動させるブロック1個の重さ
r1 = HANKEI;
w1 = 0;
hb = 10000; //10000メートルは、gが変化しないとする
w2 = 0;
ct1 = 0;
while(1){
//地球全体の位置エネルギーを求める
x = r1; //中心から地表の距離(地表は徐々に削られていく)
w1 = 0;
while (1){
//物体1個の位置エネルギーを求める
//地表から徐々に持ち上げていく
g = (GA * m1) / pow(x,2);
w1 += m2 * g * hb; //位置エネルギー
x += hb; //x は g を変化させる
if( x >= (HANKEI + US) ) break; //この長さは、r1には影響されない
}
w2 += w1; //ブロックごとの位置エネルギーを合計する
//---------ここから次の物体の計算------------
m1 -= m2; //全体の質量から、1ブロックの質量が減っていく
if( m1 < 0 ) break; //重さが小さくなったら終了
r1 = 0.03515 * pow(m1,(1.0 / 3)); //地球の質量から地球の半径を求める(地球の質量は徐々に削られていく)
//係数0.03515は、質量から半径を求めるためのもの(球の質量と半径の関係から簡単に求められる)
ct1 += 1;
}
m_edit01=w2; //計算結果 2.24366862714557e+032
UpdateData(FALSE);
予想通りの結果が出ました。
次は一般相対性理論を使って地球の全静止重力エネルギー計算します。 地球は重力のために、時空が縮んで質量が増加しています。 質量の増加分をエネルギーに換算すると、上記の2つの計算結果と同じ値になるはずです。
double GA, HANKEI, OMOSA, t1, cs, g, US, vs1, rs, rt;
double w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w13, hb;
double PAI;
double MITUDO;
double mas; //中心からの距離内の重さ
PAI = 3.14159;
GA = 6.674 * pow(10,-11); //万有引力定数
US = 5000000000; //重力の影響があまりない地点(無限遠方のつもり)と地表との距離(メートル)
HANKEI = 6.378 * pow(10,6); //地球の半径(メートル)
OMOSA = 5.974 * pow(10,24); //地球の質量(キログラム)
cs = 3 * pow(10,8); //光の速度(メートル/秒)
MITUDO = OMOSA / ((4.0 / 3) * PAI * pow(HANKEI,3));
m_edit02 = MITUDO; //地球の平均密度
hb = 10000; //10000メートルは、gが変化しないとする
rt = HANKEI;
w11 = 0;
while (1){
vs1 = 0; //初速は0
rs = HANKEI + US; //空間が歪んでないと設定した地点と地球の中心との距離(初期値)。物体が落下する距離
//地表からさらに下に落下するときの地球の重さは、その地点までの球の重さ
//物体が地面の中まで落下するまでは、rt は地球の半径
mas = ((4.0 / 3) * PAI * pow(rt,3)) * MITUDO; //初期値
g = GA * (mas / pow(rs,2)); //重力加速度 '初期値
t1 = sqrt((2 * hb) / g); //距離 hb を落下する経過時間の初期値
while (1){
//1個の物体の落下
g = GA * (mas / pow(rs,2)); //重力加速度
vs1 += g * t1; //現時点での速度
rs -= hb; //分割された1ブロックを落下する
t1 = hb / vs1; //落下距離は一定なので、速度から経過時間を求める
if(rs <= rt) break; //rs が rt の位置まで落下したら1個のブロックの速度測定は終了
}
//ここから質量エネルギーの計算をする
//物体が地表まで到達した以降が計算の対象になる
//ローレンツ変換
w1 = pow(vs1,2) / pow(cs,2);
w2 = 1 - w1;
w3 = sqrt(w2);
w4 = 1.0 / w3;
w5 = w4 - 1; //質量が増加した割合
w6 = (4.0 / 3) * PAI * pow(rs,3); //落下地点の球の体積
w7 = (4.0 / 3) * PAI * pow((rs - hb),3);//落下地点から1ブロック下の球の体積
w8 = w6 - w7; //1ブロック落下した分の球核の体積
w9 = w8 * MITUDO; //1ブロック落下した分の球核の質量
w10 = w9 * w5; //1ブロック落下した分の球核の部分が、重力場のために増加した分の質量
w11 += w10; //増加分の質量を加算する
rt -= hb;
if(rt < 0) break;
}
m_edit03=w11; //増加した質量
m_edit04 = w11 / OMOSA; //増加した質量/元の質量
w13 = w11 * pow(cs,2); //増加した質量をエネルギーに換算する
m_edit05 = w13; //計算結果 2.24105638853746e+032
UpdateData(FALSE);
予想通りの結果が出ました。
2つのシミュレーションの結果から、式[29]に1/2をかけると、静止重力のエネルギーの密度の式[35]になるという仮説が正しいことが分かります。 [35] 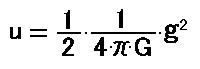
ここで行った一般相対性理論の計算は、今まで、中学生レベルの数学で一般相対性理論の問題を解く方法と「重力加速度」を「時空の伸縮」と関係付けるで使いましたが、よく分からないという問い合わせをいくつかもらいました。 確かに、特殊相対性理論と一般相対性理論の関係がはっきり分からなければ、プログラムのソースをいくら見ても、分からないかもしれません。 多くの人が、特殊相対性理論は中学校や高等学校レベルの普通の数学で解くのに対して、一般相対性理論はリーマン幾何学を使ってしか解けないと思っています。 しかし、リーマン幾何学は簡単に理解できるものではありません。 そのため、多くの人が、特殊相対性理論と一般相対性理論は、難易度レベルが非常に違うものだと思っています。 しかし、実際は、特殊相対性理論と一般相対性理論の物理的なレベルは大差ありません。 そこで、一般相対性理論を簡単に理解するためのヒントを与えます。 よく、特殊相対性理論の入門書で、時間と空間の伸縮を解説するために、列車を使った思考実験が紹介されています。 次のような内容です。 線路の横に人が立っていて、列車がそこを通過します。 線路の横に立っている人と、列車の中央の位置が一致した時点で、列車の中で、列車の中央から、前方と後方に同時に光を発射します。 すると、列車の中では、列車の前方と後方に同時に光が到達しますが、列車の外にいる人が見ると、列車の後方に光が早く到達します。 なぜこのようなことが起こるかというと、光の速度は、どのような状態で計っても一定だからです。 ここまでが、特殊相対性理論です。 この思考実験では、列車は等速度で移動しましたが、列車が等加速度で移動すると、一般相対性理論の計算式を考えることが出来ます。 等速度と等加速度では何が違うかというと、違いは、観測時間の間隔だけです。 短い時間では、等加速度運動を等速度運動と考えることが出来ます。 つまり、短い時間ごとに区切って、時間と空間の伸縮を特殊相対性理論で考えると、一般相対性理論の計算式になります。 そして、加速度と重力は区別出来ないという等価原理を使うと、重力の問題が扱えるようになります。 相対性理論を作った当時の人たちに、なぜこのような発想法がなかったかというと、当時はパソコンがなかったからです。 パソコンがないと、難解な数学に頼るしかありません。 さらに困ったことに、ある数式にたどり着いたとしても、パソコンでシミュレーションすることが出来ないので、その数式が正しいのか間違っているのか分からないということになります。 重力のエネルギーの伝わり方 [21][23]を見ると、gR は距離の2乗で減衰します。 gT は距離の1乗で減衰します。 つまり、距離が短い間は gR の方が強く、距離が長くなると gT の方が強くなり、遠方までエネルギーを運びます。 なぜそのようになるかを、今度は図[16]から説明します。 gR は球対称に全ての方向に同じエネルギーを放射するのに対して、gT には指向性があります。 質量の運動方向には、エネルギーを放射せず、運動方向と垂直の方向に最大のエネルギーを放射します。 このことが、エネルギーの減衰の仕組みに関係しています。 運動方向と垂直の方向に最大のエネルギーを放射するということは、もし質量が単振動をする場合は、放出するエネルギーは横波になります。 このエネルギーを波として観測すると、重力波になります。 地球の公転により放出する重力エネルギーを計算 
に次の値を代入します。 
計算すると 2.117×10^9 ワットになります。 地球の公転による運動エネルギーは、2.7×10^33ジュールなので、1億年で運動エネルギーの10億分の2が、重力波として放出されることになります。 |
戻る