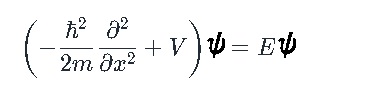
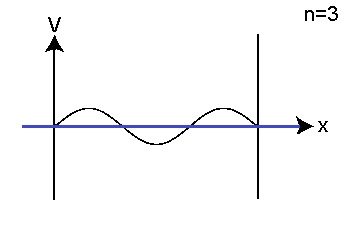
シュレディンガー方程式をコンピュータで解く はじめに 電子のシュレディンガー方程式を、コンピュータで解くプログラムを紹介します。 １次元の時間に依存しないシュレディンガー方程式を使って、井戸型ポテンシャルの波動関数とエネルギーを求めます。 下記のシュレディンガー方程式を使います コンピュータで解く前の準備として、下図のような井戸型ポテンシャルを解析的に解きます。 ポテンシャルは、-a<x<aでは、V＝0 ｘ<=-a かつ a<=x では、V=∞ a は 10nm です。 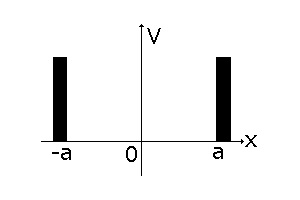ポテンシャルが 0 なので、シュレディンガー方程式は下記のようになります。 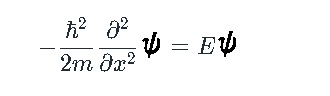波動関数を下記のように予想します。 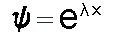波動関数を２回微分します。 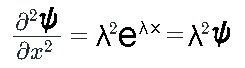これをシュレディンガー方程式に代入します。 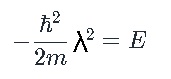λの値は下記のようになります。 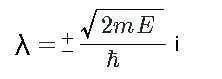波動方程式の一般解は下記のようになります。 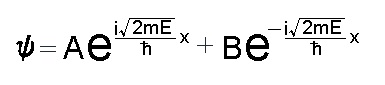-a と a では波動関数の値は 0 なので下記のようになります。 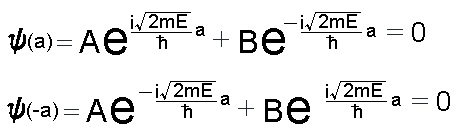上式から波動関数とエネルギーを求めると下記のようになります。 （式の変形は、少し複雑なので説明を省略します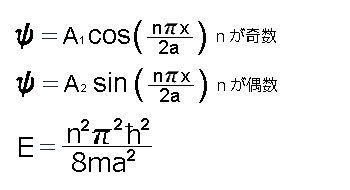） 上式から波動関数の形を描き、エネルギーを計算します。 n=1 では E=0.94meV n=2 では E=3.76meV n=3 では E=8.46meV となります。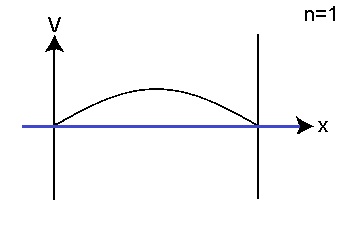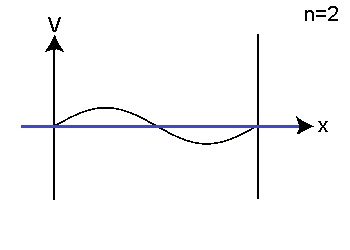 今度は、コンピュータを使って、波動関数の形とエネルギーを求めます。 ソフトを起動します。 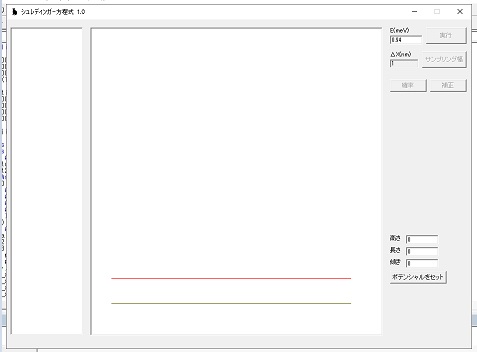「高さ」「長さ」「傾き」を 0 のままで「ポテンシャルをセット」ボタンを押します。 E(meV)は 0.94、サンプリング幅は 1nm で、「実行」ボタンを押します。 （0.94 は前回シュレディンガー方程式を解析的に解いた n=1 の値と同じです。） 左のリストにはポテンシャルと波動関数の値が表示されます。右には波動関数の形が表示されます。（波動関数は規格化されていません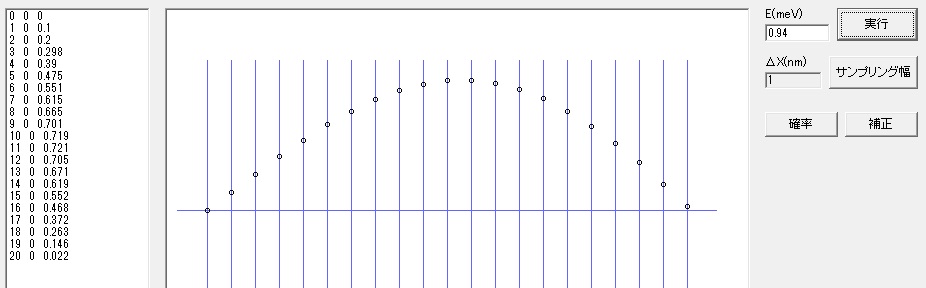） 次に、サンプリング幅を 0.5nm にします。 下記のように「サンプリング幅」「ポテンシャルをセット」「実行」の順にボタンを押します。 サンプリング幅が 0.5nm の波動関数が表示されます。 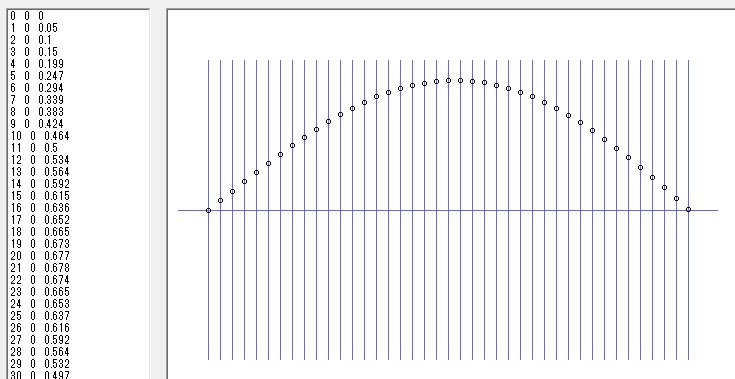次に、サンプリング幅を 0.25nm にします。 下記のように「サンプリング幅」「ポテンシャルをセット」「実行」の順にボタンを押します。 サンプリング幅が 0.25nm の波動関数が表示されます。 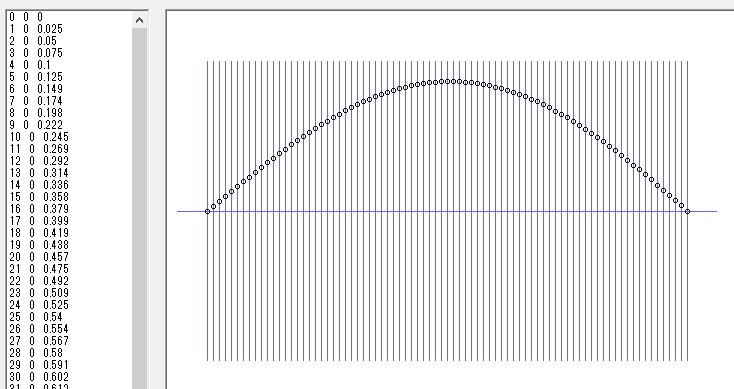「確率」ボタンを押すと、電子の存在確率を示す曲線が表示されます。 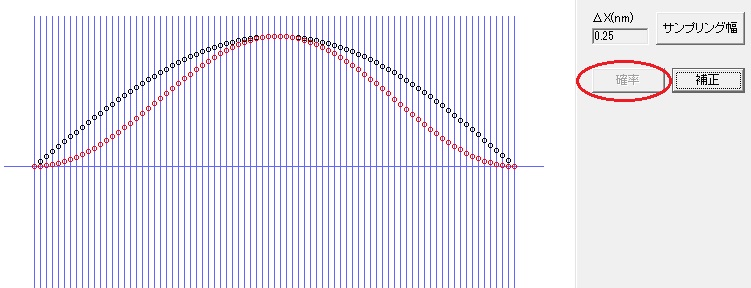E(meV) に 3.76 と書き込み「実行」ボタンを押します。 （3.76 は前回シュレディンガー方程式を解析的に解いた n=2 の値と同じです。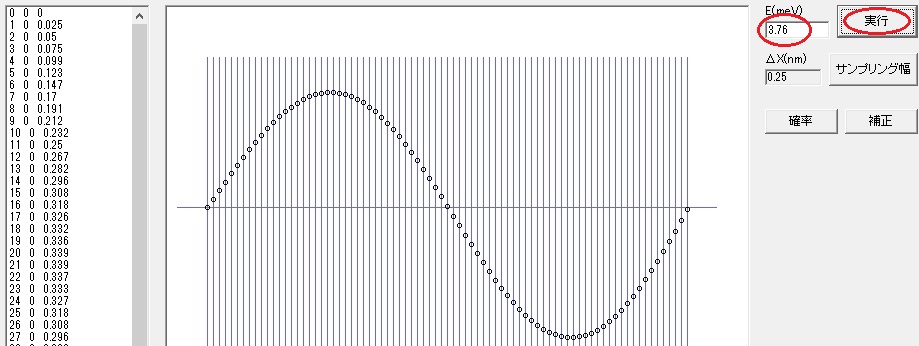） E(meV) に 8.46 と書き込み「実行」ボタンを押します。 （8.46 は前回シュレディンガー方程式を解析的に解いた n=3 の値と同じです。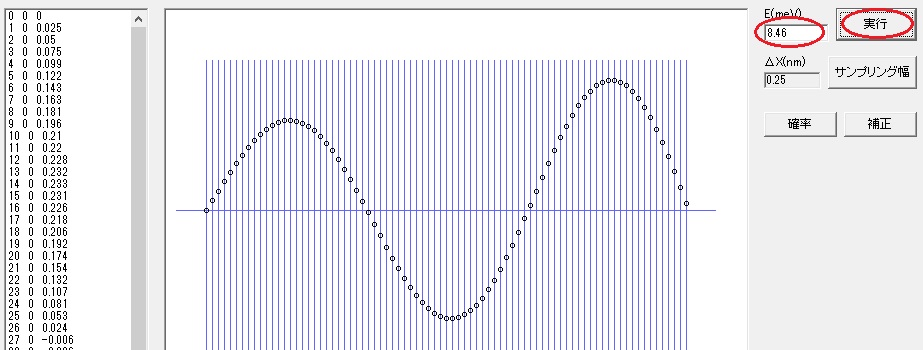） 波形が複雑になると、誤差が積み重なってくるため「補正」ボタンを押して、誤差の修正を行います。 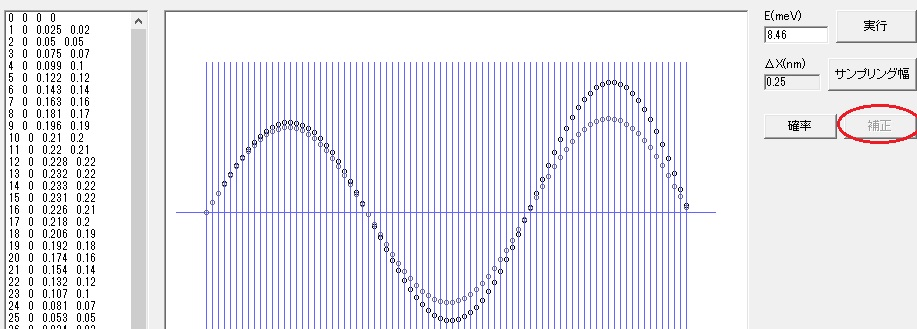「確率」ボタンを押すと、電子の存在確率を示す曲線が表示されます。 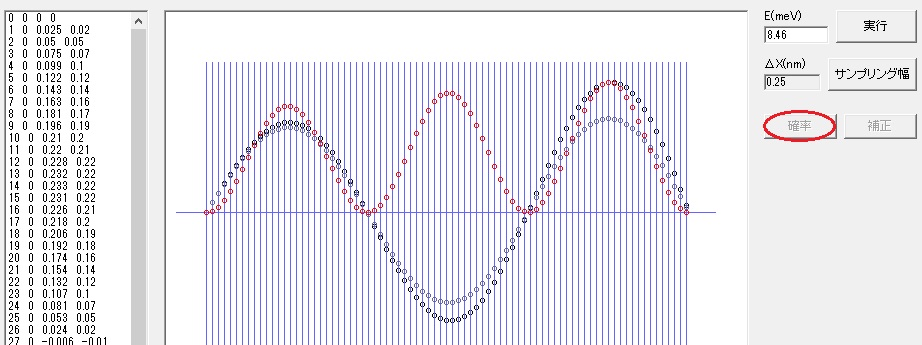サンプリング幅を 0.25nm で、「高さ」50、 「長さ」0.25、「傾き」0 に設定します。 下図のように、この井戸型ポテンシャルは左右対称になっています。 左右の端は V=∞ 中央は V=0 一段上は「高さ」で設定します。 「高さ」50 とは 50meV のことです。 「長さ」0.25 とは、井戸の全長の 25パーセントを意味します。（全長は 20nm です） 左右の端からそれぞれ、25パーセントを１段高くします。 「傾き」0 は外から電場がかかってない状態を示します。 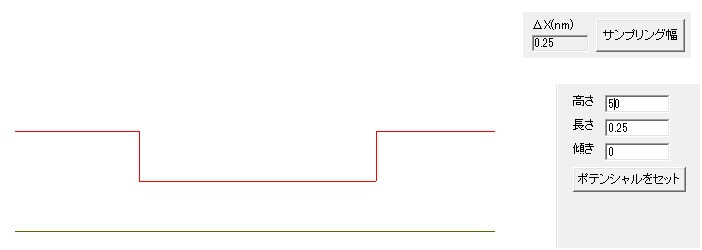全領域でポテンシャルが 0 のときは E(meV)=0.94 で波動関数の右端は 0 に収束しました。 今回の状態で E(meV)=0.94 にして「実行」ボタンを押すと下記のようになります。 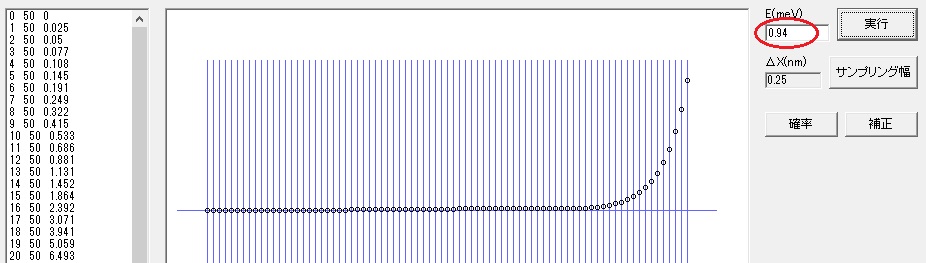E(meV)の値を予想します。2 にして「実行」ボタンを押すと下記のようになります。 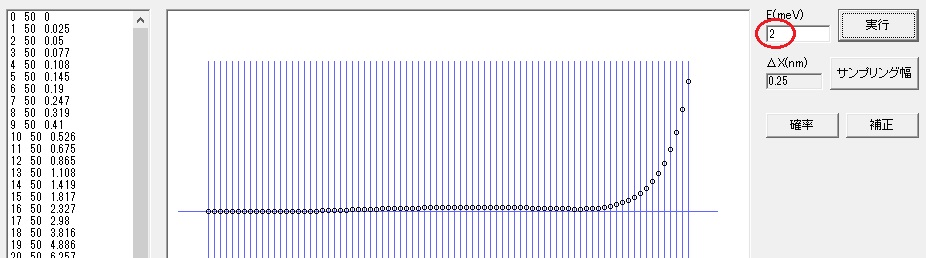あまり改善されないので 3 にして「実行」ボタンを押すと下記のようになります。 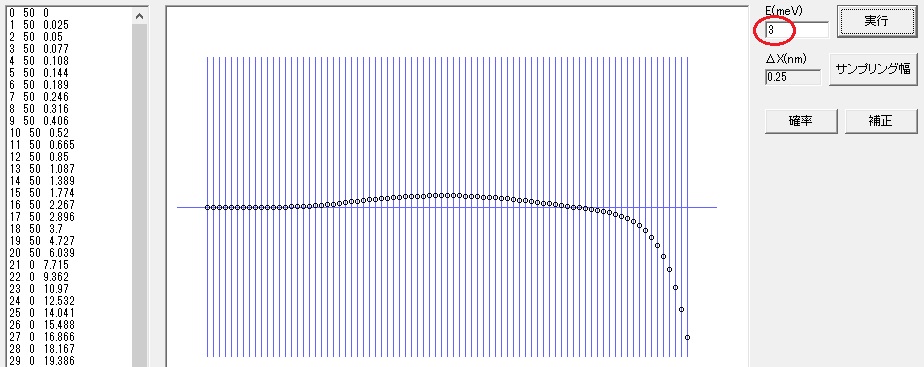今度は右端が下がりすぎたので 2.5 にして「実行」ボタンを押すと下記のようになります。 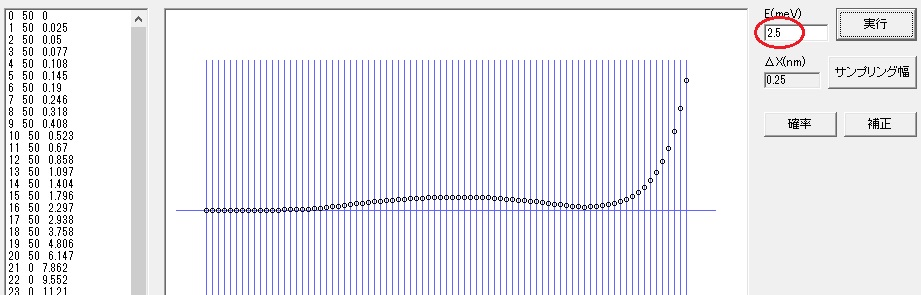数回、微調整を行うと E(meV)=2.727 で右端が0 になります。 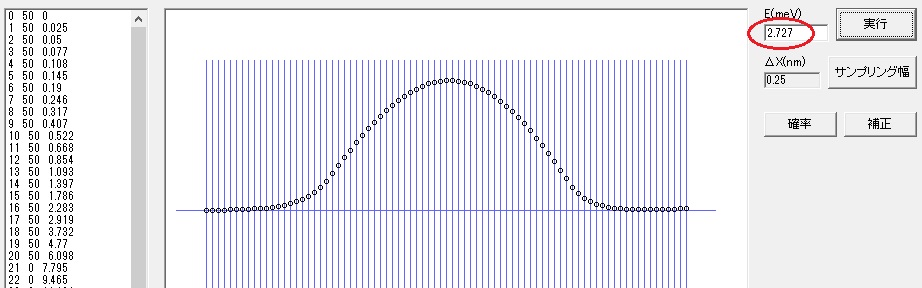「傾き」を 4 にし、「実行」ボタンを押します。 「傾き」が 4 とは、右端が +4meV 左端が -4meV になり、全体のポテンシャルが斜めに傾いた状態になります。 前回と同じ E(meV)=2.727 では右端が 0 にならないので、調整を行います。 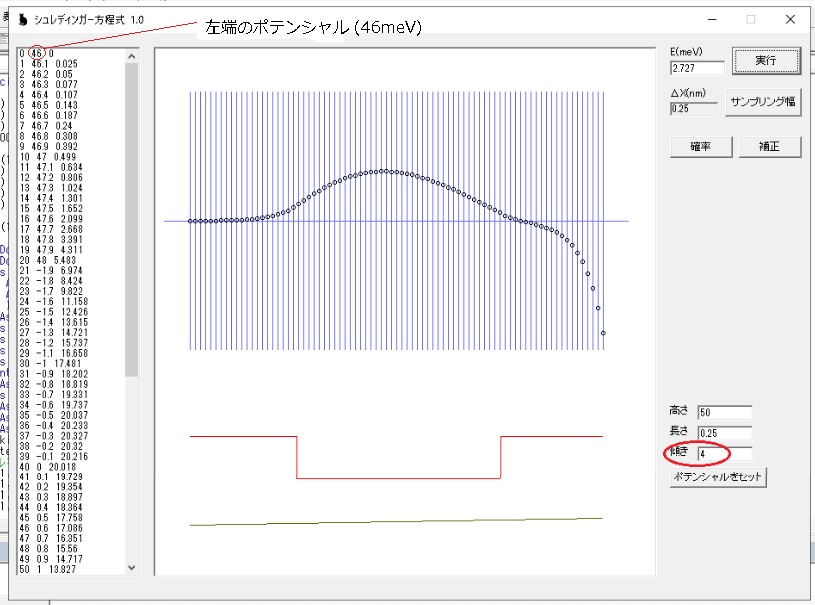E(meV)を 2.7 にすると下記のようになります。 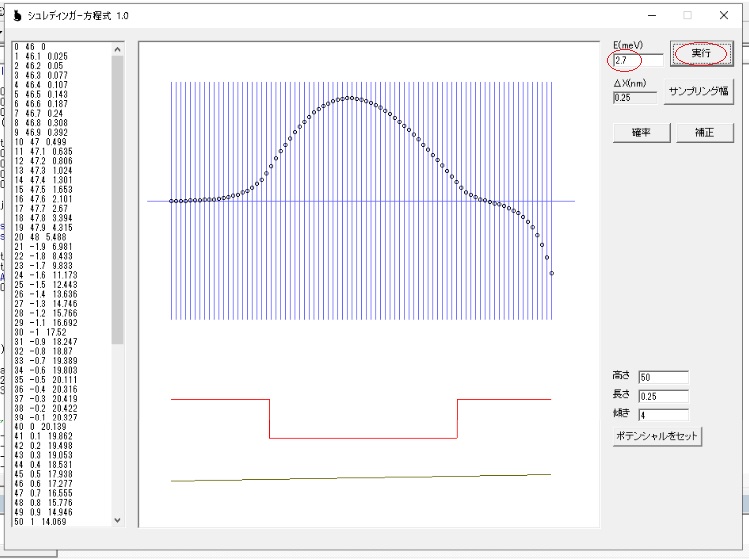数回、微調整を行うと E(meV)=2.6877 で右端が0 になります。 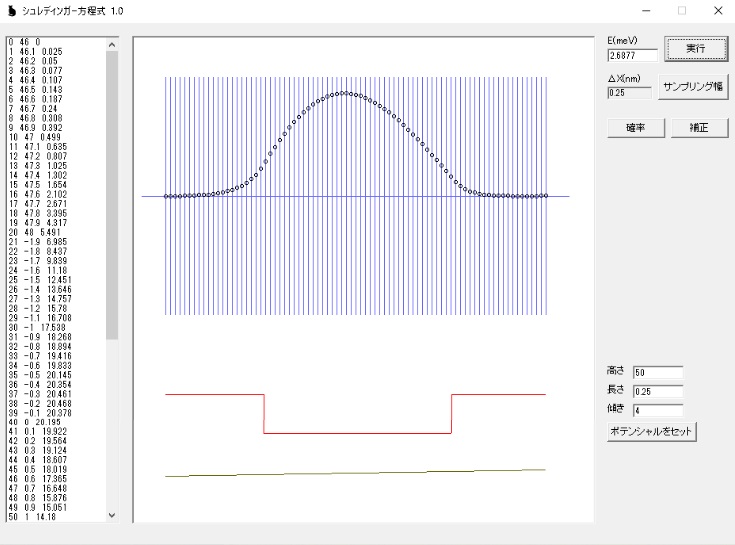プログラムの仕組み まず、２次の微分方程式�@を２つの１次の微分方程式�A�Bに置き換えます。 １次の微分方程式をコンピュータが処理できるように差分方程式に置き換えます。 ２つの差分方程式を繰り返し計算すことで波動関数を求めます。 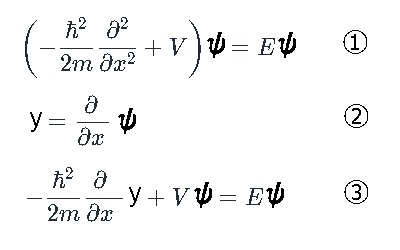おわりに 「確率」ボタンを押すと、電子の存在確率曲線が表示されますが、存在確率について解説します。 電子は観測するまでは、波として存在してますが、観測すると、一瞬で粒子に変化することが分かっています。 これを波束の収束と言いますが、この理論を採用すると、物理現象が非常に複雑になります。 なぜなら、未来の現象が過去に影響を与えることが可能になるからです。 この現象を回避するために、多数の並行宇宙の存在を考えます。 そうすると、存在確率とは波束が収束する位置の確率ではなく、観測者の意識がどの並行宇宙を選択するかの確率になります。 では現実はどうなっているのでしょうか。 実は「現実」というものがあるのか無いのかは誰にも分からないのです。 「現実」があったとしても、１つだけなのか、多数あるのか誰にも分かりません。 また「現実」「幻想」「夢」の違いを明確に区別ができる保証もありません。 確実なことは、「自分」には意識があり、世界を体験しているということだけです。 つまり、宇宙が１つ存在するのか、多数の並行宇宙が存在するのかは、考えやすい方を選べばよいだけです。

Vector ソフトライブラリ
シュレディンガー方程式 Ver1.0 をダウンロード


戻る