|
量子論多世界解釈での意識とは何か
2017/8/18 まず、結論を先に述べます。 ●宇宙は、一つ一つの静止した宇宙が多数集まって出来ています。 ●静止宇宙の数は、無限ではなく有限です。 静止宇宙の数は、宇宙の中で素粒子の組み合わせの数だけあります。 ●意識は、アルゴリズムで作ることは出来ません。 したがって意識は、宇宙の外に存在します。 宇宙の外というのは、3次元立体は2次元平面の外にあるのと同様に、3+n次元は3次元の外にあるという意味です。 ●時間は、意識の焦点が多数の静止宇宙を移動することによって生じます。 移動は量子エンタングルメントする静止宇宙の間で可能なので、複数の移動経路があります。 したがって、時間は直線的ではありません。 ●過去は変化する。 過去とは、静止宇宙の人間の脳の中のデータ(記憶)のことです。 このデータは、どの静止宇宙に意識の焦点が移動するかによって、いくらでも変わります。 ●物理法則の根本的な見直しが必要になります。 重力などの自然の法則は、意識の焦点が移動することで生じます。 重力は、意識の焦点が重力の法則を満たすような静止宇宙を選んで移動することで生じます。 意識が物質の世界には存在しないことを説明します。 多くの人は、人間の脳と同じ能力を持つコンピュータが出現すれば、コンピュータは意識を持つことが出来ると考えています。 現在、一部の仕事でAIが人間に代わって仕事をしています。 簡単な会話なら、相手が人間なのかコンピュータなのか分かりません。 このAIに10億倍の処理能力を持たせると、人間とかなり複雑な会話をしても、相手が人間なのかコンピュータなのか分からないでしょう。 この場合、このコンピュータは意識を持っていると考える人もいるでしょう。 しかし、コンピュータが意識を持つとは考えられない理由があります。 一般に、意識には段階があると考えられています。 人間よりも、犬は意識が弱いし、昆虫はさらに意識が弱いと。 もし、コンピュータが突然意識をもつとすれば、その意識は人間のレベルなのか、昆虫のレベルなのかが問題になります。 コンピュータが、突然人間と同じレベルの意識を持つのは不自然ですし、人間と同等な会話をするコンピュータが昆虫レベルの意識を持っているというのも不自然です。 人間の脳は理論的には、コンピュータで再現できます。 コンピュータは、考えることとが出来ますし、感情を表現することも出来ます。 しかし、今説明したように、コンピュータは、自分が考えていることと自分の感情を意識することは出来ません。 アインシュタインは、重力による力と、加速度による力を区別する手段が無い場合、両方を同じものとしてよいとする等価原理を考えました。 これは、画期的な思考法です。 この手法を「人間は夢と現実を区別する方法があるのか」という問題に使います。 人間には、今意識している世界が夢なのか夢から覚めた状態なのか証明する手段はありません。 一般的には、人間の意識は夢と現実の2つの世界を認識するだけだと考えられています。 しかし、現実と考えられている世界も、別の意識状態からは夢と考えられる可能性があります。 別の意識状態を覚えてないのは、夢の中で眠っていることに気がついていないのと同じです。 等価原理をまねると、この問題は次のようになります。 意識が認識する世界を、全て夢と考えます。 そこで次のような結論が導き出されます。 夢の中の登場人物は、あなたが作り出したもので意識を持っていません。 夢の中のあなたも、あなたが作り出したもので意識を持っていません。 夢の世界全てをあなたが作っています。(夢の中のあなたではありません) これを、現実と考えられている世界にも当てはめてみると、他人も自分も意識を持っていないことが分かります。 先ほど、コンピュータは意識を持つことがないと結論ずけたのですが、結局人間も意識を持たないということです。 これで「将来、コンピュータが意識を持つことになるのか」などと心配する必要はなくなります。 意識とは、宇宙を外から観察している「何か」なのです。 多世界解釈での静止宇宙の数はどのくらいか? 計算方法は、宇宙全体をプランク長の立方体で区切り、宇宙全体の素粒子をプランク長の立方体に割り当てる組み合わせの数になります。 ただし、宇宙の体積を正確に求めることは現時点では不可能です。 なぜなら、重力の強い空間と弱い空間とでは、プランク長がかなり違うからです。 宇宙全体のプランク長は、ほとんど分かっていません。 そういう訳で、素粒子の組み合わせだけで静止宇宙の数を求めました。(宇宙の体積を計算に入れると、さらに大きな数になります) 全宇宙の中の素粒子の数が 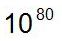 、素粒子の種類(パリティなどを考慮)を20とすると、静止宇宙の数は 、素粒子の種類(パリティなどを考慮)を20とすると、静止宇宙の数は
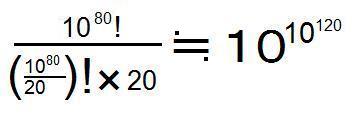 となります。 となります。
これがどのくらい大きな数かというと、 例えば、将棋のパターン数は 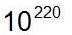 ですが、このくらいの数なら指数を使わずに紙に書くことは可能です。(1の後に0を220個書けばよいのです。) ですが、このくらいの数なら指数を使わずに紙に書くことは可能です。(1の後に0を220個書けばよいのです。)
しかし、静止宇宙の数は指数を使わずに紙に書くことは原理的に不可能です。 なぜなら、1の後に0を 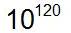 個書かなければならなず、宇宙の全物質を使っても0を書くための紙を作ることが出来ないからです。 個書かなければならなず、宇宙の全物質を使っても0を書くための紙を作ることが出来ないからです。
|
戻る