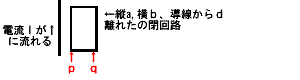基本の流れ↓これが電磁気Ⅱ基本的にはこれだけのようなもの!!!ちゃんと把握しとくように!!!ここに書いてあることはすべて
『たぶん…』
です。いっさい責任など負いません。
これは電磁気2においてとても大事な基本事項です。後期勉強したことなんてこんなもんしかありません。後はあななたちが持っている数学の知識でとけるはず。ここに書いてある式の一つ一つには意味があるので覚えましょう。
|
第1段階 ま、愛なんだよね… |
2. ビオ・サバール 大事!一問くらいコレ使った問題で出る気もします。だから問題下にのせます、 でも余談で一番大事なのはベクトルポテンシャルよrotA=Bの!むふふふ。ま、君たちには関係ないか・・・ |
3 与えられている!!! ならそのまま次の2段階へGO! |
第2段階 磁束を求める のような場合点p、qで導線の電流から生じる電界が等しくないので横方向のみ積分する。縦方向は横が一定ならどこも同じ磁界の強さになる。 |
第三段階 別に-の符号があったっていいじゃないか
とてもくさい。 φ←自分のすった屁(磁界;とてもくさい)= MI←他人の屁 |
アンペアの周回積分の問題
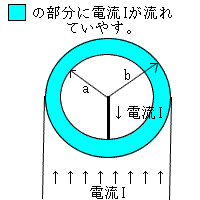
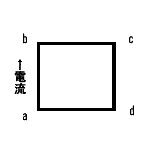
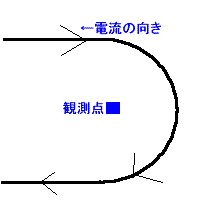
図↑のように半径bの無限直線導体があり、その中心から半径aは空洞になっている。また、電流は矢印の方向に青の部分にI[A]一様に流れています。(電流密度を考える。もし導体表面・・・なら密度は考えない。)また、中心部にも無限長直線導線があり↓向きにI[A]流れています。 問1 半径0<r<aの単位長さあたり(縦1mって事)の磁界を求めよ 解答 基本は無限長の線なので、アンペルの周回積分を使います!んで、積分路を考えたとき、その中にある磁界のみの電流に着目する!
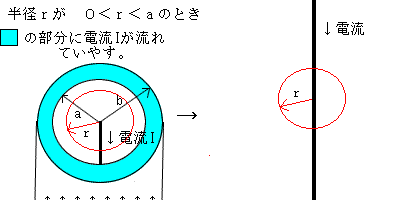
図のように、半径r(範囲が 0<r<aになるような)の積分路赤を考えます。そうするその積分路の中の電流のみに着目する決まり(理由はあるけど)なので右図のようになります。 よって ∫H・dl=I ←(積分路内の電流はI[A]のみ、 dlっていうのは半径rの円の積分路の微小長さ!だからdlを積分すると半径rの円になって2πrなんよ♪) ∫H・dl=∫Hdlcos0°=∫Hdl=H∫dl (dlを積分すると半径rの円になります。磁界の強さも半径rの円方向になり、大きさはその円部分はどこも同じになるので定数と考えられHは∫の外にだせる。) =H2πr=I となりHを求めると H=I/2πr ここで磁束密度は B=μH より B=μI/2πr 問2 半径a<r<bの磁界を求めよ a<r<bのような半径rの積分路を考える。
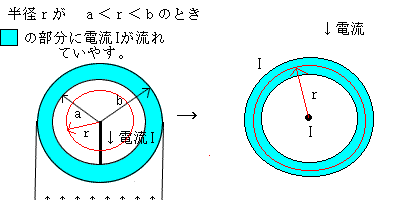
↑こっちね♪ ここでこの半径rの中にある電流は中心部の導線の電流Iと導体の電流Iとなります。ここで導体部分は一様に電流Iが流れているので(導体表面に電流が流れている問題だとこの後考える電流密度は考えない)導体部分の電流密度を考える。 まず青色の面積Sを考える。 S=πb^2(外側の円の面積)ーπa^2(内側の円の面積)=π(b^2-a^2) よって青色の電流密度Jは J=I/S=I/(π(b^2-a^2)) [A/m^2] ←長さを1[m]と考える。問題より単位長さあたりだから! だから半径r内の導体部分全電流は I導体=J×面積=I/(π(b^2-a^2))×π(r^2-a^2)=I(r^2-a^2)/(b^2-a^2) よって半径r内の全電流(導体と導線)は 全電流I=I(導線)+(-I導体)=I-I(r^2-a^2)/(b^2-a^2) ←流れている方向がぎゃくだから。どっちを-としても良いよ よってアンペルの周回積分は ∫H・dl=全電流I=I-I(r^2-a^2)/(b^2-a^2) ∫H・dl=∫Hdlcos0°=H∫dl=H2πr=I-I(r^2-a^2)/(b^2-a^2) H=・・・ 自分で計算して・・・ ってこんなごちゃごちゃしたかなぁ・・・ 間違ってたら悪いね☆ってあってるけど。もしr=bだったら電流は0になるからあってます。 電流の方向は、導体にI[A]流れてて、導線に同じだけの電流I[A]流れています。んで導体はI(r^2-a^2)/(b^2-a^2)[A]流れてて、r=bだとI[A]流れるけど条件がa<r<bなのでI[A]以下しか流れてないことがわかります。だからこの場合合計で半径r内には下に電流が流れていることがわかるよね。よって時計回りが磁界の方向です。 問3 半径b<rの磁界を求めよ b<rの条件をみたす半径rの積分路を考えるとその中の全電流は ∫H・dl=全電流=IーI=0 となるのでHも0です!!! |
導線2本の問題・・・ 交信中・・・ |
↑の応用問題例題!!! 図のような無限長の導線に電流Iが流れています。その直線から半径方向dに縦a,横bの閉路があります。 2. 閉路を貫く磁束を求めなさい(2段階) つまづいたっていいじゃないか……… 3. 相互インダクタンスを求めなさい(第3段階)(この場合直線無限導線の電流Iより発生した磁界(他人の屁)が別の閉回路を貫く磁束(私のお鼻♪キャン…)の関係、だから… ) 貫く総磁束がN倍!!! φ1=Nφより φ1=MI ほら、Mがより大きくなる!つまりチョウ~ く♪さ♪い♪ 4. また、電流IがI=Irm sinωt のとき閉回路に発生する起電力を求めよ。(第3段階)(こんなときは閉回路に抵抗があるよん) 終了 今もわからない… 計算があってっかはわからんけど多分あってる!考え方は多分あってる。これがでるかはわからんがだいたいアンペアの周回積分 磁束求めるとき片方積分 相互インダクタンス 誘起起電力とまぁ、たくさんの基礎使うからだしただけ。 |
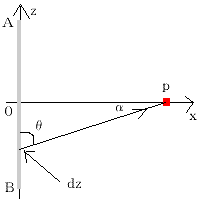
ビオサバールの問題 図のような一辺の長さ2aの正四角形に電流が矢印の方向に流れています。
解答 だから例題8.5(教科書)といっしょ! 基本はdzは電流の流れる方向とその微少長さ!(こんかい電流はz軸上にがれているのでdz。これがx軸上だったらdxになります~ どれでも表せない曲線や次の例題などは dl ってあらわします) rはその電流の微少長さの部分から観測点(測りたい場所)までの位置ベクトル ベクトルのままでも円筒座標を用いれば単位ベクトルで計算できるが、教科書がちがうので教科書通りにいきます。
a/r=sinθ=cosα ・・・このようにすると、θ、L、rなどの変数がα一つで表せるからしたんだよ。 H=∫dH
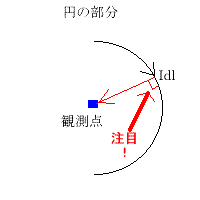
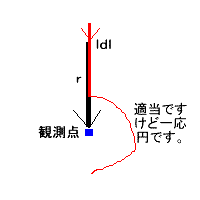
これが正三角形なら3倍。正8角形なら8倍です~♪ 問 教科書演習のp215のような問い8.4は円の部分だけ考えればOK なぜなら、ビオサバールは(へんな形→ビオちゃん 最初の決まり事参照) dB=μI/(4π)dl×r/r^3←(rの三乗の事 です。) ここで注目 dl×r があります。dlは電流の方向です(こんかい直線、そして円という経路をとるためzなどの軸上におけないので dl としたんだよ)。rはその電流から測りたい磁界までの距離ベクトルです。これらは dl×r=dl r sinθn←これはdlとrが作る面の法線方向(90°方向)の単位ベクトル だから円の部分はぜ~んぶθ=90になります。
直線部分はぜ~んぶdlの方向と、rの方向が同じなんでθ=0°となります。だから直線部分の磁界はゼロです。
んなもんで答えは式(8.36)の半分かにゃ!半径のながさが同じなら! 演習でやった形
は直線部分はp191の例題8.5と同じ!ただし半分で♪んでも2個あるから2倍で同じか・・・ rの方向と電流の流れる方向が違うから磁界は0じゃないんだよねぇ!
θ → シータ → ……………
ばず~!!!!!!!!!!!! しぃぃぃぃぃぃぃーーーーーーーーーたぁぁぁぁぁぁぁ!!! 僕の大好きな『ラピュタより…』 ラブラブですね… |
ちからの問題。考え方!!!
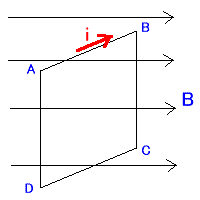
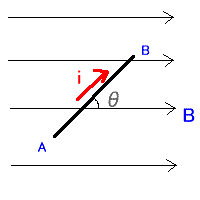
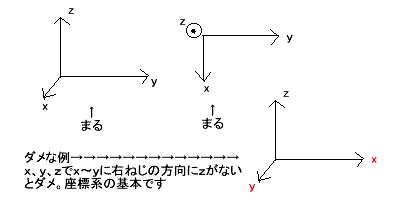
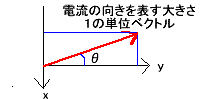
図の用に一様に磁界Bが矢印の方向で発生している。その磁界中に一辺Lの正四角形の閉路がおかれている。そしてiアンペアの電流が流れています。磁界の方向と閉路はθずれています。 はじめに・・・ まず、図をちゃんと把握すること!右の図は、左の図を真上から見ているんだよ!!! そして、座標系を上図(まるってかいてあるやつ二つ!問題の図におのおの対応しています)しめします。ここで『ダメな例』をよく覚えとくこと! 問1 AB, BC, CD, DAの力のベクトルを求めよ。 解答 公式 F=(I×B)L より ○ABについて 座標系右と問題右図より考えます。そうすると、磁界は B=Bj (|B|=B←つまり磁界の大きさ♪、 j は、y方向の単位ベクトル) そして電流は I = I (- i sinθ+j cosθ) (↑図からわかるように赤は電流の単位ベクトル。それをθを使ってx、yの i jの成分に分割する! ) よって、公式より F=(I × B)L={I (- i sinθ+j cosθ)×Bj}L =IBL(- i sinθ+j cosθ)×j =IBL(- zsinθ)=-IBLsinθz ○CDについて ABと電流の向きが変わるだけなので I = -I (- j sinθ+y cosθ) ←上の電流に-つけただけ F=(I × B)L={-I (- i sinθ+j cosθ)×Bj}L =-IBL(- i sinθ+j cosθ)×j =-IBL(- ksinθ)=IBLsinθk ○BCについて(問題図、座標左参照) 磁界は B=Bj 電流は I=I(-k) 公式より F=(I × B)L={I (- k)×Bj}L =IBL(- k)×j=IBLi ○DAについて BCのぎゃく!!!!(電流の向きが逆で磁界の向きが同じだからわかるでしょう書かなくても!) まとめ ってなふうにフレミングの左手で確かめても同じようになったでしょう!先に大きさ求めても(例題8,10)いいけどね!コレの方がわかりやすいはず。ただねぇ、座標系が ぱっ!ってでてきて、ちゃんと電流とかわかれば・・・ この問題に対しては、どの(x、y、z)軸でもいいんだけど代表して、方向の変わらない磁界の方向をy軸方向としました。 |
最後にながれ!!!
1、磁界(磁束密度)を求める! 無限長ならアンペア、有限、円、四角ならビオちゃん。与えられてたらラッキーちゃちゃちゃ♪ ・・・はぁ。
2、磁界(磁束密度)より閉路内の磁束を求める! 距離により変化するなら積分!磁束が一様ならそのまま面積かける!!!
3、あとはインダクタンス、誘起起電力を公式からブチこむ!
以上!!!
問題予想というか・・・ でそうな問題というか全部だけど簡単にまとめて書くと! 1問目 語句の穴埋め!定義などその式の意味、今までに書いたことちゃんと呼んで理解していればだいたい解るはず 2問目 ビオ・サバールを使う問題!HPに載せた問題で十分な気がします。 3問目 磁気回路の問題か、ソレノイドの問題。HPに乗せてないけど教科書の問題で十分です。 4問目 self or matuale inductance(自己、相互インダクタンス)スペルあってるかわかんないけど・・・ か、誘起起電力の問題。 5問目 力、モーメントの問題教科書の例題で十分。←もしかしたら語句ででるかも・・・。 だいたいこんな感じ!ただ、俺は試験問題など一切しらないので責任はもたないけど。まぁ、がんばって、
|
この前質問うけた感じの答えです。後大事なのは磁気回路p206 これは例題みたいな問題で十分でしょう!決まった感じなんで簡単です。あとソレノイド!自己インダクタンス、相互インダクタンスでこの問題がでるかも・・・ 、また二本の導線!力!後は定義!言葉、誘起起電力とか、自己インダクタンスとか相互インダクタンスとか・・・ あとなんだろ・・・ 磁束密度? 磁界? わかんない問題あったら連絡してこ~い!気が向いたら解答書くよ・・・
でも・・・ いつも誰からも頼られないから… 頼られると弱いんだよね・・・
あ、あと 間違ってたらまじおしえて!大変な事になりそうだから!優秀軍団君よ!ほんとマジで!結構適当だからおれ
もうちょい更新します♪日曜くらいまでには・・・ だからがんばってちょ~♪
2年生のみなさんへ!(特に火、土組♪)
も、もう・・・ みんなと会うことはなくなるかもしれないけど・・・ 先生・・・
先生・・・
みんなのこと決して忘れないから~(>o<)/~~~~~~~~~~~~~~~~ エーン
あのみんなで分かち合った喜び!そして感動を・・・ 君たちと会えてとてもいい学生生活に終止符を打てたと思うよ。
君たちと出会ったのは春に散る・・・ そんな桜の木の下だったよね。まだ、高校のあどけなさが残るなか・・・ きみ達が出会ったこと・・ いまでも 私の胸の中には鮮明にその光景が残っているよ・・・。そして笑顔でかわす日々・・・ 楽しかった・・・。大好きだよ・・・ 電磁気単位とってね♪それが俺の幸せでもあり・・・ 君たちの幸せにもつながるんだから・・・
んなこたぁ一欠片も思ってません
か、感想なんか送ってくれると・・・
ちょっと嬉しいなぁ・・・
べ、別に暇人なんかじゃないよ~