長篠の合戦

　「長篠の合戦」と言えば信長の火縄銃３段撃ちが有名であるが、これは文献を盲目的に 信じた人間の発言力が強かっただけのことであり、実際にはありえなかったことであると 断言できる。従来検討されることのなかった視点から捉えて以下に記す。

１）銃砲の射撃法
　本論に入る前に射撃の基本知識として、是非とも知っておくべきことがある。複数の銃 砲を発射する場合の射撃法としては、指令に基づいて全ての銃砲を同時に発射する「一斉 射撃」と、個々に目標を定めて発射する「各個射撃」とがある。あるいは特定の区域に多 数の弾丸を撃ち込み、その中の何発かが有効弾となれば良しとする「公算射撃」と、一発 必中の精神で射撃する「狙撃」とに分類することもできる。
　「公算射撃」は主に曲射弾道を利用するもので、間接照準によって射撃に必要なデータ を計算し、発射諸元を砲側に伝えて射撃を行うものである。野戦における砲兵戦や水上艦 同士の遠距離砲戦が代表的なもので、小銃の場合にはあり得ない射撃法である。特に艦砲 による遠距離砲戦の場合には弾着を観測して射撃データを修正するので、「一斉射撃」で なければ効果的な射撃とはなり得ない。
　一方「狙撃」は直接目標を狙って撃つもので、小銃や戦車砲が代表的なものと言える。 個々に目標を狙って撃つのだから必然的に「各個射撃」となり、指令による「一斉射撃」 は戦闘開始の時以外にはあり得ない。火縄銃も兵器としては小銃であるから、基本的な射 法としては「狙撃」であり、「各個射撃」でなければ効果的な射撃となり得ない。現在で は個人携行火器でも全自動の小銃や短機関銃等があり、公算射撃的な発射法もあり得るが、 火縄銃の場合には狙撃以外はありえない。伝えられる信長の３段撃ちでは毎回一斉射撃と なる訳だが、これは小銃の使い方としては全く理に反したものなのである。

２）３段撃ちの可能性と有効性
　従来から言われている「３段撃ち」の場合には、３隊に分かれた各隊は「一斉射撃」を 行って順次入れ替わることとされている。
　先ず最初に生ずる大きな疑問点は、戦闘開始時の第１射はともかく、第２射以降の「一 斉射撃」はどのように行うのか、と言うことである。射撃を終えた兵士と入れ替わって戦 闘位置についた全ての兵士の照準完了を、どのように把握するのであろうか。もし一定時 間が経過したら無条件に号令を発するのであれば、まだ照準をつけていない兵士は全くの 無駄弾を発射することになる。逆に照準済みの兵士の場合には、号令が出るまで発射でき ないことになり、時間の無駄を生じることになる。人闇は機械ではない。大勢の人間が寸 分の狂いもなく、正確なサイクルで射撃することは不可能なのである。
　次は実際に「３段撃ち」が実行されたものとして、射撃サイクルについて検討してみる こととする。文献によれば装填時間は２５秒程度とされているが、入れ替わり・索敵・照 準に必要な時間を５秒と仮定しても、１回の射撃サイクルは３０秒となる。３隊に分かれ ていれば各隊の射撃闇隔は１０秒となるので、指揮官は１０秒経過したら自動的に射撃指 令を出すようにすれば、従来の「３段撃ち」も可能だと思われるかも知れない。しかし実 際には装填時闇には個人差があり、「一斉射撃」を行うためには最も遅い兵に合わせる必 要がある。更には入れ替わりや目標の設定・照準にも個人差があるので、１回の射撃サイ クルはさらに数秒延びることとなる。しかもこれは鉄砲の数が少ない場合の話であり、三 千挺もの数になれば話は全く異なったものとなる。
　実際に鉄砲の数が三干挺であったとすれば、各隊の鉄砲は一千挺となるが、これだけの 数の鉄砲を横一線に配置しようと思えば、戦線の長さは２ｋｍ程度は必要かと思われる。 単純に計算すれば各人の間隔は２ｍであるから、あるいは大きすぎると思われるかも知れ ない。しかし装填作業を行っている兵は二千人であるから、横に並んだ各兵の間隔は１ｍ に過ぎない。縦に並んで装填作業を行えばもっと狭まるが、その場合には入れ替わる時に 混乱する可能性がある。さらに戦場の第一線には鉄砲足軽以外の配員も必要であり、重い 鉄砲を抱えて入れ替わることを考えれば、このくらいの空間は必要ではないだろうか。射 撃指揮官が戦線の中央にいたとしても、片側の戦線は１ｋｍもの長さになり、一斉射撃の 号令を発しても、末端に号令が届くのは３秒後となってしまうのである。
　組織的に入れ替わるためには移動にも号令が必要となるが、この号令にしても末端に届 くには３秒が消費されることになるし、末端からの射撃完了、あるいは移動完了の合図を 指揮官に送る場合にも、やはり同様の時間が必要となるのである。実際の戦場においては 末端まで号令を確実に伝達すること自体も困難かと思われるが、順調に号令が伝わったと しても、号令の伝達だけで１０数秒の時間が必要なのである。
　旗等を振って視覚による合図で時闇のロスを防ぐことも考えられるが、火縄銃の射撃に よる硝煙等の影響を考えれば信頼性に欠けるし、各兵への伝達は旗を見た現場指揮官の号 令に頼ることになるので、とても実戦的な方法であるとは思えない。結局一干挺もの大量 の火縄銃で「一斉射撃」を行うためには、号令伝達等による時間のロスが多く、混乱なく 順調に号令が伝わったとしても、１回の射撃サイクルに必要な時間は５０秒以上になると 予想され、各隊の射撃間隔は２０秒近い時間が必要となる。さらに火縄銃では不発や暴発 も珍しくはなかったようであるから、この点も考慮するならば「一斉射撃」を行うための 消費時間はさらに増え、通説の「３段撃ち」は極めて現実離れした射撃法であると言わざ るを得ない。
　一千挺の「一斉射撃」が不可能ならば、百挺ずつ１０隊に分け（鉄砲は各隊三百挺とな る）、各隊毎に「３段撃ち」を行う方法も考えられる。百挺ならば号令伝達による時間の ロスは遥かに少なくなり、２ｋｍもの戦線全体に対して一斉に攻撃をかけてくることも考 えられないので、より現実的な射撃法であると考えられる。ではさらに細かく分けて、十 挺ずつ１００隊としたらどうだろうか、あるいは更に細かく分けて一挺ずつ１０００隊と したらどうなるだろうか。
　一挺ずつと言うことは「各個射撃」であり、個人で発射を決定する「狙撃」となるので 号令は必要なくなる。すなわち仮に「３段撃ち」が行われたとしても、射撃自体は「一斉 射撃」よりも「各個射撃」の方が効果的であることになる。しかし戦場という特殊な状況 下において、個人々々の判断で射手がスムーズに入れ替わり、混乱もなく「３段撃ち」を 持続するためには、非常に高いレベルの兵が必要となる。当然寄せ集めの足軽部隊では不 可能であり、精鋭を集めて組織化された鉄砲部隊を編制し、普段から十分に訓練を行って おく必要がある。兵農分離を実行した信長ならば専用の鉄砲部隊の編制は可能かも知れな いが、当時にあっては弾薬類は貴重晶であったと思われる。多数の兵士に常時十分な射撃 訓練を行わせることは、不可能であったことと思われる。
　結論としては、従来から言われている一千挺の鉄砲隊が順次入れ替わり射撃する「３段 撃ち」は、全く実現不可能な射撃法ではないにしても、極めて効率の悪い射撃法であり、 実戦で用いられたとは考えられない。

３）火縄銃の空白時間について
　火縄銃３段撃ちの概念が生まれた背景には、火縄銃は弾込めに時間がかかるので、その 隙に敵の突進を受けると対処できない、という発想がある。このこと自体は間違いではな いのだが、銃の装填時間を利用して突進するという考え方は１対１の場合には適用できた としても、千・万単位の集団による戦闘の場合には、全く異なったものとして考えなけれ ばならないのである。
　実戦で一千挺もの大量の鉄砲を使用して射撃した場合、先ず最初に一千発の弾丸が発射 され、２５〜３０秒の空白時間をおいて再び一千発の弾丸が発射される、と言うような状 況は考えられない。装填に要する時間にも個人差があるが、実戦では目標を見つけて照準 に至るまでの時間にも、大きな個人差が発生するものと考えられる。各射手の次回発射ま でに要する時間が各々異なるのであるから、実際の戦闘においては２５〜３０秒毎に一千 挺の鉄砲が発射されるのではなく、絶え間無くどれかの鉄砲が発射されているというのが、 実際の状況であると思われる。
　一千挺の鉄砲を横一線に並べ、入れ替わることなくその場で「各個射撃」を行った場合 の射撃状況を、パソコンを使ってシミュレートしたことがある。射撃の条件としては、装 填に要する時間は２５秒、個人差による装填時間の延長を最大５秒、さらに照準・射撃に 要する時闇を０〜５秒と仮定した。この条件で次回の発射に要する時間を式で表せば、
　Ｔ＝２５＋（６×乱数１）十（６×乱数２）　　　（０≦乱数＜１）
となり、最短で２５秒、最長で３５秒となる。射撃法は戦闘開始と同時に一千挺を撃つの ではなく、最初の発射は二百挺のみとし、以後５秒毎に二百挺ずつ発射することとした。 各射手は第２射以降は自分目身の判断で狙撃することになるが、第２射以降の発射弾数を １秒単位で集計した結果、発射弾数に相違はあるものの、装填による空白時間は発生しな かった。最初のうちこそ多少の山谷があって発射弾数の少ない時もあるが、時間の経過と 共に平均化されていき、何れの時刻にも満遍なく発射されるようになる。
　シミュレーションを行ったのは１０数年前のことであるが、参考までに使用したパソコ ンとプログラムを文末に紹介しておく。プログラムの移植は容易であろうから、自分自身 で確かめることも可能である。処理速度は昔のパソコンでも問題ないし、言語はＢＡＳＩ Ｃで十分である。ただ注意しなければならないのは、パソコンの乱数は擬似乱数なので、 初期値が同じだと毎回同じ結果となってしまう。適当に乱数のタイミングをずらしてやれ ば、色々なパターンを見ることが出来る。

４）「３段撃ち」と「各個射撃」の比較
　一千挺の鉄砲で「各個射撃」を行った場合、前記シミュレーションでは３分間の発射弾 数は約５８００発となった。次に三千挺の鉄砲で「３段撃ち」を行った場合であるが、発 射闇隔を２０秒と仮定しても発射弾数は９０００発に過ぎない。すなわち３倍の鉄砲を使 って「３段撃ち」を行っても、その発射弾数は「各個射撃」の５割増しに過ぎないのであ るから、「３段撃ち」は効率の悪い射撃法であると言わざるを得ない。さらに「３段撃ち」 では十分な照準が得られないまま発射する場合も含んでいるのであるから、実際に有効な 弾数は９０００発よりも少ないものとなる。また「各個射撃」の場合には射手が入れ替わ るための空間は必要ないので、射手間隔を狭めて銃の密度を高めることも出来る。しかも 運用の柔軟性は「３段撃ち」に比べて遥かに優るので、脅威の大小に応じての戦力の増減 も容易に実行できる。重点区域に迅速に兵力を移動できることは、実戦では大きな利点と なるものと考えられる。

５）「３段撃ち」の新説
　仮に「３段撃ち」というものが存在した場合、通説のように射手が入れ替わるのではな く、鉄砲だけが移動する方法を考えてみた。
　三千挺の鉄砲を３隊に分けるのは従来と同じであるが、最前列の人間は射撃専用の兵と して射撃を終えても後方には下がらない。射撃した鉄砲は後方の兵に手渡し、代わりに装 填済みの鉄砲を受け取って前方の敵に対して攻撃を行う。もちろん第２射以降は「各個射 撃」となるので、号令の伝達による時間のロスもないし、人間が入れ替わる時の混乱の発 生も考える必要はない。三挺の鉄砲に対して射手が１人と装填手が２人、この編成を最小 単位として一干隊三干挺の鉄砲を配備するのである。
　この方法ならば、従来型「３段撃ち」に対して数多くの利点がある。先ずは射撃法が小 銃の基本である「各個射撃」になるため、号令伝達による時間のロスもなく、十分に照準 して効果的な「狙撃」を実行できることになる。各射手はその場で射撃に専念することが できるので、常に敵情を把握して容易に攻撃目標を設定することが出来る。後方で自ら装 填して射撃位置につく場合に比べて、心理的な余裕は遥かに大きなものとなり、その余裕 は射撃精度にも大きく影響するものと考えられる。同様に装填手の場合にも装填に専念で きるので、落着いてより確実に装填することができるはずであり、不発弾が発生した場合 でも処理は容易だと思われる。さらには命中精度の高い兵を専用射手として選択すること により、より多くの有効弾が期待できるであろう。
　この方法の特徴は射手と装填手とを「分業」させたことにあるが、このような思想は当 時としては考えられなかったことと思われる。しかし通説の「３段撃ち」よりも遥かに効 果的な射撃法なので、あえて紹介した次第である。

　文献の信頼性とは如何程のものであろうか。近くは前大戦においても、真実とはかけ離 れた「大本営発表」なるものが多々存在したようである。メディアの発達した現在におい ては、偽りの情報を流すことは極めて容易なことである。テレビカメラの捕らえる映像は ごく一部の範囲であり、周囲の状況を視聴者が知ることは出来ない。テレビ画面に映し出 される映像が真実なのか演出されたものなのか、それを判断するのは古文書を解読するよ り難しいかもしれないのである。


「射撃シミュレーション」
　　二百挺ずつの５隊が５秒間隔で射撃、射撃開始２５秒後からの発射弾数

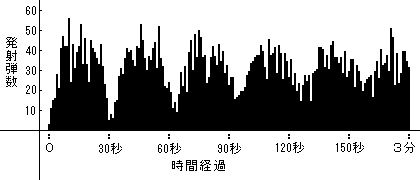
「射撃シミュレーション」プログラム
　（使用パソコン：Ｘ６８０００、言語：Ｘ−ＢＡＳＩＣ）

 100 dim int tf(1000),fn(180)
 120 int t=0,gn=1,fg=0
 130 for i=1 to 900:rnd():next
 140 shoki()
 200 repeat
 205   fn(t)=0
 210   repeat
 220     if tf(gn)=0 then fire() else tf(gn)=tf(gn)-1
 290     gn=gn+1
 300   until gn=1001
 304   fg=fg+fn(t)
 305   inji()
 306   t=t+1:gn=1
 310 until t=181
 320 lprint:lprint "合計発射弾数";fg;"発"
 900 end
1000 func shoki()
1010 int a=0,gs=1
1020 repeat
1030   repeat
1040     tf(gs)=(a*5)+(rnd()*6)+(rnd()*6)
1050     gs=gs+1
1060   until gs=201+a*200
1070   a=a+1
1080 until a=5
1090 endfunc
2000 func fire()
2010   fn(t)=fn(t)+1
2020   tf(gn)=25+(rnd()*6)+(rnd()*6)
2030 endfunc
2100 func inji()
2110   lprint using "###秒後";t;
2120   lprint using "####発";fn(t);
2140   for i=1 to fn(t):lprint "*";:next
2160 endfunc

 130行の値を変えることで、乱数の初期値を変えるようにした。

　艨艟トップへ