|
ブラックホールとは、非常に強い重力のため、シュヴァルツシルト半径より内側では脱出速度が光速を超え、光ですら外に出てくることが出来ない天体のことです。
地球の質量を一点に集中すると0.5センチの半径以内がブラックホールになると言われています。 太陽の質量を一点に集中すると3キロメートルの半径以内がブラックホールになると言われています。 しかし、実際にはシュヴァルツシルト半径とブラックホールは存在しません。 今からそれを説明します。 |
|
これから述べることは、特殊相対性理論の基礎を理解している人が対象です。
(特殊相対性理論の解説書は山ほどあり、中学生以上なら誰でも理解できます) 特殊相対性理論は、完全に正しい理論です。 なぜなら、どのような慣性系から見ても、光の速度が一定になるということは、宇宙には特別な中心が無いということと、等価だからです。 特殊相対性理論の計算式を算出するのに、よく、等速度運動をする列車が使われます。 地面に静止している人に対して、列車の長さの半分の位置が重なったときに、光を列車の前後に発車するという思考実験です。 日常の感覚では、列車が走っているため、列車内の人と地面に立っている人では、光の速度が異なって観測されるはずです。 ところが、特殊相対性理論では、光の速度は列車に乗っている人が観測しても、地面に立っている人が観測しても同じ値になります。 この現象を解決するためには、時間と空間を伸縮しなければなりません。 上の例では、列車が等速度運動をしていましたが、こんどは列車が加速度運動をしている場合を考えます。 同じように、地面に静止している人に対して、列車の長さの半分の位置が重なったときに、光を列車の前後に発車します。 この場合も、地面に静止している人に対しても、列車の中の人に対しても光は同じ速度になります。 加速度運動の場合は、時間を小刻みにして、短い時間の間は、列車は等速度運動をすると考えます。 一般相対性理論の計算式は、等速度運動を加速度運動に拡張したものです。 つまり、特殊相対性理論の計算式を積分したものが一般相対性理論の計算式になります。 さらに、一般相対性理論では、重力と加速度を同じ現象と考え、重力の問題を加速度の問題にすり替えて解くことが出来ます。 これを等価原理といいます。 ここまでは、一般相対性理論は、非常に整然とした美しい理論になっています。 ところがです。 これから先に一般相対性理論に間違った部分が出てきます。 一般相対性理論を数式化するのに、複雑で難解なリーマン幾何学を使っため、アインシュタインを初め、多くの研究者がリーマン幾何学に消化不良を起こします。 特殊相対性理論によると、物体がどれだけ加速されても、光の速度を超えることはありません。 特殊相対性理論を積分することによる一般相対性理論でも、物体がどれだけ加速されても光の速度を超えることがありません。 このことを、等価原理を使って重力に置き換えると、どんなに強い重力でも光を止めることは出来ないということと等価になります。 つまり、光が脱出できないシュバルツシルト半径は存在しないことになります。 だいいち、シュバルツシルト半径が、ニュートン力学を使った方法と、一般相対性理論から導かれたシュバルツシルトの方法とで、同じ値になることが、すでにおかしいのです。(太陽の質量は一点に集中した場合のシュバルツシルト半径は約3Kmになるとされている) なぜなら、ニュートン力学を使った方法では、太陽の質量が一点に集中した場合に、時空は全く伸縮しないからです。 多くの書物には、シュバルツシルト半径に近づくと、時間が遅れると書いてありますが、空間の縮みについては書かれていません。 相対性理論の最も基本的な原理は、時間と空間が同じ割合で伸縮するということです。 だからこそ光の速度は、誰が観測しても同じになるのです。 巨大な質量が一点に集中した場合のミンコフスキー図は下記のようなイメージになります。 分かりやすいように、中心からの距離を、3つの層に分けて表示しています。(実際の計算では多くの層に分割します) 3つの層のいずれも光の速度を一定にするように、時空が伸縮されているのが分かります。 この図を見ると、時空の伸縮は非常にシンプルで、シュバルツシルト半径が出現する余地は全くありません。 
一般相対性理論ををリーマン幾何学で記述する場合、どのような状況でも、光の速度を一定にするように時間と空間を一対として考える必要があります。 よくあるブラックホールの話では、時間と空間が無関係に伸び縮みしますが、そのようなことは絶対に起こりません。 まして、シュバルツシルト半径内では、時間と空間の役割が逆になるなどは、言っている本人も訳が分らないのではないでしょうか。 物理学は、まず目的の現象を、イメージでビジュアル化する必要があります。 ブラックホールは、具体的なイメージがないまま、消化不良の数式に振り回された結果、生み出された架空の物体です。 |
|
ニュートン力学を使ってシュヴァルツシルト半径を求める、間違った方法
まず、シュヴァルツシルト半径を求める計算式を使って、太陽の質量が一点に集中した場合のシュヴァルツシルト半径を求めてみます。 シュヴァルツシルト半径は、第二宇宙速度(脱出速度)を求める式を使います。 脱出速度が光の速度になった時点の半径がシュヴァルツシルト半径です。 <第二宇宙速度(脱出速度)を求める式> まず、地球からロケットを発射する場合の脱出速度を求めます。 地球の遠方を基準にして、質量mの物体の地表の位置エネルギーは、 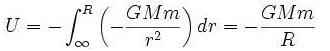
で表せます。 Uの値と運動エネルギーが等しくなったときの速度が脱出速度です。 
この式に、次の値を代入して計算すると、脱出速度は、11.2Km/sになります。 
この式を変形します。 
ここで、Mに太陽の質量(1.99×10^30Kg)、vに光の速度(3×10^8m/s)を入れると、Rは、2.95Kmになります。 確かに、太陽の質量を一点に集中すると、約半径3Kmのブラックホールになります。 しかし、この式は間違っています。 |
|
ニュートン力学による脱出速度を求める数式は、光よりもかなり遅い物体には使えますが、光に近い速度を持つ物体や光そのものには使えません。
この式は、下記のことが考慮されていません。 ●光の速度は常に一定。 ●重力の影響で時間はゆっくり進む。 ●重力の影響で空間は縮む。 これらのことを考慮した、私の発明した方法で、太陽の質量が作るとされる半径3キロのブラックホールを調べてみます。 この方法は、以前「中学生レベルの数学で一般相対性理論の問題を解く方法」で紹介したもの(人工衛星と地上の時間のずれを計算)を少し変更したものです。 発表してすぐに、かなり反響があり、多くのメールをいただきました。 最も多かったのは「人工衛星と地上の時間のずれを高い精度で計算するのはすばらしいのですが、式の意味が良く分からない」というものです。 そこで、今回、式の意味を詳しく説明します。 人工衛星と地上の時間のずれを計算するプログラム Dim GA, hankei, omosa, px, t1, t2, t3, c, p, g, u, v, r As Double Dim bunkatu, i As Long GA = 6.67 * 10 ^ -11 '万有引力定数 px = 100 '分割された1ブロックの長さ(メートル) u = 20000000 '人工衛星と地表との距離(メートル) hankei = 6.378 * 10 ^ 6 '地球の半径(メートル) omosa = 5.974 * 10 ^ 24 '地球の質量(キログラム) bunkatu = u / px '分割数 c = 3 * 10 ^ 8 '光の速度(メートル/秒) t1 = px / c '静止系(地球に対して止まっている)での測定時間(光が、分割された1ブロックを走る時間)。 v = 0 '等価原理を使い、重力を、ロケットの加速度から生じる引力に置き換える。ロケットの初速は0。 r = hankei + u '人工衛星と地球の中心との距離。 't1 は、静止系(地球に対して止まっている)から観測した、分割された1ブロックを光が走る時間(この時間は一定)。 't2 はロケットの中での経過時間で、ロケットの速度が速くなるほど時間が遅れてくる。 't3 は、分割された1ブロックを光が走る時間の差(静止系とロケット系との時間の差)。 For i = 0 To bunkatu - 1 g = GA * (omosa / r ^ 2) v = v + g * t1 '等価原理を使い、重力を、ロケットの加速度から生じる引力に置き換える。ロケットの最終速度。 r = r - px Next i t2 = (t1 - v * px / c ^ 2) / Sqr(1 - (v ^ 2 / c ^ 2)) 'ロケットの中での経過時間。 t3 = t1 - t2 '最後の遅れが、求める遅れ。 Text1.Text = t3 * (1 / t1) '1秒ではどれほど遅れるか。 結果 5.26317633122293E-10 地表は上空よりも1秒間に5.26E-10秒、時間が遅れます。 <プログラムのやっていること> 地球上では重力が働いて、地球の中心に引っ張られますが、これは、ロケットに乗って宇宙空間を加速しているときにロケットの床に引っ張られるのと同じことだと考えることが出来ます。(等価原理といいます) そういうわけで、プログラムでは、地球に働く重力を、ロケットに乗った人に働く加速度による引力に置き換えて計算します。 計算には、特殊相対性理論の公式を使います。 特殊相対性理論の公式は、加速度の無い空間でしか使えないと思っている人が多いと思いますが、加速度のある場合でも、短い時間で狭い空間では、特殊相対性理論の公式が使えます。 特殊相対性理論を加速度系に拡張したものが一般相対性理論ですが、具体的には、特殊相対性理論の式を積分したものが一般相対性理論の式になります。 幸いに現在では、100年前と違い、パソコンがあるので、難解な数学的な手法を使わなくてすみます。 プログラムの説明 For i = 0 To bunkatu - 1 g = GA * (omosa / r ^ 2) '(1) v = v + g * t1 '(2) r = r - px Next i t2 = (t1 - v * px / c ^ 2) / Sqr(1 - (v ^ 2 / c ^ 2)) '(3) t3 = t1 - t2 '(4) Text1.Text = t3 * (1 / t1) '(5) (1) g = GA * (omosa / r ^ 2) この式は、重力加速度を求める式です。 重力加速度「g」は地表では、約9.8m^2/sですが、地球の中心からの距離が変化すると、「g」の値も変化します。 (2) v = v + g * t1 この式にある「t1」は、「px」の距離を光が走る時間です。 「g * t1」は、「重力加速度×「px」の距離を光が走る時間」で、物体が一定の時間(非常に短い)に加速されたために生じる速度を表します。 「v = v + g * t1」は、前回計算した速度を加えています。 この計算を「bunkatu - 1」だけ繰り返します。 「v」は、光が20000000mの距離を進む時間の間に、重力加速度の影響で生じる物体の最終速度です。物体が地表から20000000mの距離を落下した時点の最終速度ではありません。 (3) t2 = (t1 - v * px / c ^ 2) / Sqr(1 - (v ^ 2 / c ^ 2)) ローレンツ変換の公式を使って時間の遅れを計算しています。 (4) t3 = t1 - t2 t1は、光が重力が無い空間を一定距離走った場合の所要時間。 t2は、重力の存在する空間を一定距離走った場合の所要時間。 t3は、重力による時間の遅れ。 (5) Text1.Text = t3 * (1 / t1) t3は、分割した1ブロックを光が走る間の時間の遅れなので、1秒間にはどれだけ遅れるかを計算しています。 |
|
太陽の質量が一点に集中した場合にできると言われているのが半径3Kmのブラックーホールですが、半径2Km地点の時間の遅れを計算します
Dim GA, hankei, omosa, px, t1, t2, t3, c, p, g, u, v, r As Double Dim bunkatu, i As Long GA = 6.67 * 10 ^ -11 '万有引力定数 px = 100 '分割された1ブロックの長さ(メートル) omosa = 1.9884 * 10 ^ 30 '太陽の質量(キログラム) 6.96 * 10 ^ 8 '太陽の半径 hankei = 2000 '中心からの距離(メートル) u = r - hankei '光が走る距離(メートル) bunkatu = u / px '分割数 c = 3 * 10 ^ 8 '光の速度(メートル/秒) t1 = px / c '静止系での測定時間(光が、分割された1ブロックを走る時間)。 v = 0 '等価原理を使い、重力を、ロケットの加速度から生じる引力に置き換える。ロケットの初速は0。 't1 は、静止系から観測した、分割された1ブロックを光が走る時間(この時間は一定)。 't2 はロケットの中での経過時間で、ロケットの速度が速くなるほど時間が遅れてくる。 't3 は、分割された1ブロックを光が走る時間の差(静止系とロケット系との時間の差)。 For i = 0 To bunkatu - 1 g = GA * (omosa / r ^ 2) v = v + g * t1 '等価原理を使い、重力を、ロケットの加速度から生じる引力に置き換える。ロケットの最終速度。 r = r - px Next i t2 = (t1 - v * px / c ^ 2) / Sqr(1 - (v ^ 2 / c ^ 2)) 'ロケットの中での経過時間。 t3 = t1 - t2 '最後の遅れが、求める遅れ。 Text1.Text = t3 * (1 / t1) '1秒ではどれほど遅れるか。 結果 太陽の半径(6.96 * 10 ^ 8m)地点と、中心から2000m地点の時間の遅れは1秒間に約0.6秒 太陽の半径(6.96 * 10 ^ 8m)地点と、中心から3000m地点の時間の遅れは1秒間に約0.4秒 太陽の半径(6.96 * 10 ^ 8m)地点と、中心から4000m地点の時間の遅れは1秒間に約0.3秒 <結論> ブラックホールの表面では時間の進行が止まることになっていますが、そのようなことが起こらないことが分かります。 プログラムを見て分かると思いますが、時間が静止に近づくのは、シュヴァルツシルト半径ではなく、中心から無限小の距離です。 そのとき空間の長さは無限小に近づきます。 そのために、無限大に近い重力の中でも光は一定の速度で走ります。 強い重力の星は、光が赤方偏移を起こしますので暗くなりますが、完全に暗くはなりません。 深い海の底でも明るさが完全に0にならないのと同じです。 今までは、シュヴァルツシルト半径内からは、光が全く出てこないことになっていましたが、これは間違いです。 今まで、中心から距離を2Kmとか3Kmとか言っていましたが、この数値は、距離が重力によって縮まないと考えた場合の距離です。 実際には1秒間に0.4秒遅れるブロックは、0.4倍の長さに縮みます。 縮んだ全ブロックを積分した長さが、実際に観測した長さになります。 |
戻る