---

収束光中に配置した回折格子の分光


　分光観測を簡略化するために、回折格子を光学系の収束光の中へ配置する観測者がいます。　一般に分光学では、平面の回折格子を使う場合は平行光に、曲面をもった回折格子を使う場合は収束光または発散光を使います。　これらの回折格子は観測する光の進み方（または波面）にそって回折が行われるように設計されているからです。　これに従わずに、収束光の中に平面回折格子を配置して分光観測をするのは邪道なのですが、実際にはある程度観測できているという事実がありますので、否定することはできません。　収束光中に平面回折格子を置いた場合の回折効率の文献を見たことがないのですが、あるフランス人のアマチュア天文家は幾何光学的に光線追跡を行い、1次光で光が色ごとに十分分散されていることを示しています。　

　幾何学的に色が分解されても、実際にどの次数でどのくらいの割合で分光が行われているかは未知数です。　そこで回折計算を行ってみました。　この計算はもしかしたら世界初の計算かも知れません。　もし他にもこのような回折計算があるという場合には、ご一報ください。

計算仕様はいたってシンプルで、完全球面並が収束する光路中にブレーズ化された平面回折格子を配置し、焦点面での強度分布を二次元的に求めるものです。　計算仕様はシンプルでも、実際の計算自体は非常に複雑を極めます。　図を参照。

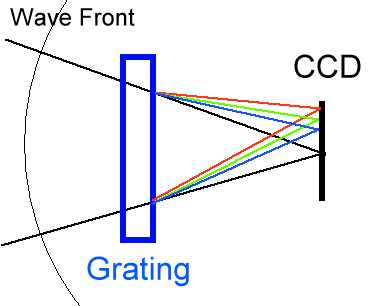計算仕様の概念図
計算条件は以下のとおり

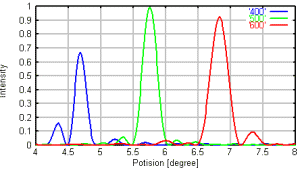
波長　：　400,500,600nm　の3波長　（グラフ中順に、青、緑、赤となる）
溝の深さ　：　500nm　で最適化
溝の間隔　：　200本/mm
明るさFno　：　Fno=4.0　と　10.0
回折格子の位置　：　CCD面より40mm手前


回折格子の配置には条件があり、ミリ200本のものを使った場合には、CCD面より50mm以内に配置しないと分光として働かないようである。　本数の少ないものを使えば、その距離は長くなる。

まず計算してみてわかったのは、平面回折格子を収束光中に配置しても上記条件を満たせば分光されるということである。　これだけも進歩があったというものでしょう。　ではどのような強度分布になっているのか見てみましょう。

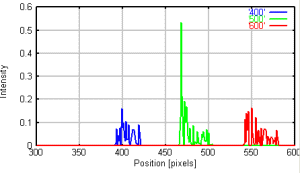
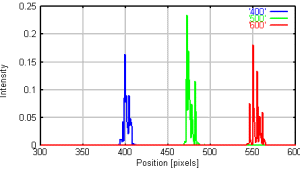　 左：F4.0の場合の分光強度分布　、　右：　F10.0の場合の分光強度分布

これを見てわかることは、暗い光学系の方がシャープな画像が得られるということである。　一般に分光は明るい光学系ほど高分解能が得られるのだが、収束光中に配置する場合は反対の性質がみえられます。　この原因は、分光強度分布が回折的に行われているのではなく、幾何学的に光が集中しているためであると考えられます。　球面で入ってきた波面は平面の回折格子と位相を揃えて回折することはありえません。　各微小な部分での分光が幾何学的に重なり合って、ある部分に集中していると考えられます。

ついでに平行光中に配置した場合の強度分布を見てみましょう。

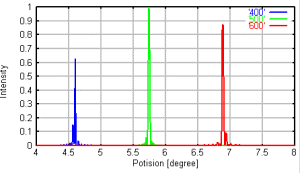
　 左：100本の溝を通過した分光強度　、　右：10本の溝を通過した分光強度

　一見して強度分布がきれいに現れ、良く知られているように、通過した溝の本数が多い分光の方が明らかにシャープであることもわかります。　明るい光学系であれば、光線が太くなり、通過する溝の本数も増えることになり分解能があがります。　収束光を使った場合と反対ですね。　ちなみに、収束光中に配置する場合、その収束光が通過する溝はなんと数百〜数千本にも及びます。　ミリ200本×十数ミリ＝数千。

ということで、簡略化された収束光中の分光でも私が思っていた以上にしっかり分光できていることがわかりました。　かといって、この方法で分光することをお勧めはいたしません。　強度分布を見ればわかるように、強度分布がやや不規則な形が出てくるために、強度の測定にはかなりの困難が待ち受けているのは明らかです。　

平行光で分光を行うには、コリメートする必要があるため、コリメートレンズと集束レンズの２つを少なくとも用意しなければならないので、光学系がやや複雑化かつ、コストが上がります。　したがって、手軽に分光をやってみたいというのであれば、CCD直前に回折格子を置いて観測するのも良いかもしれません。　

分光器の製作 9,3,2000


Astronomy
Optics

TOP

mail