---

ナイフエッジ・コリメート法によるピントだし


　デジタルカメラは銀塩一眼レフカメラのように裏ぶたを開けて直接ピント確認することができません。　CCDで直接撮像して星像を見ればいいのですが、天体撮影を意識して作られていないのでLCD表示だけでピントが出てるかどうかはっきりしません。
　そこで、デジカメのAFを信頼して何か遠くのものを直接撮像してAFしてくれればピントが出そうです。　しかし夜間に遠くて明るく大きさのある物体などはありませんので、一眼レフカメラを使って焦点像をコリメートして無限遠像を作り出します。　一眼レフカメラのフィルム位置にナイフを置いてその像をコリメートさせデジカメでAFさせる方法です。

ナイフをフィルム位置に置く
コリメートさせてお互いを覗かせる（実際には1台はデジカメ）
　手順としては、
１、一眼レフカメラの裏ぶたを開け、ナイフエッジ法でピント出しする
２、カメラを向きあせ、裏ぶた後方から面照射する
３、デジカメをAFモードしてに、ナイフのエッジにピントを合わせる
４、デジカメをMFモードにする

これで無限遠出しが簡単にできます。

ではどのような一眼レフカメラレンズを使用すればよいのでしょうか？

ここからは光学の話になりやや難しくなります。
まずレンズ1枚を用意します。　遠くの星から発した光がレンズに入射すると、決像しその位置を焦点位置を言います。　逆に、反対側にも焦点を結ぶ位置が存在します。

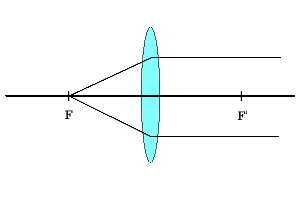遠くの点光源が位置Fに決像
次に、光学ではニュートンの式といって決像関係を表す式があり、光軸上の任意の位置から出た光がどこに決像するかを表すものです。

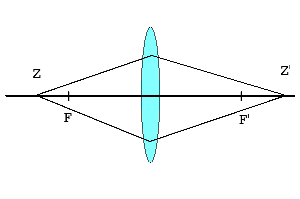ニュートンの式を表す図
上の図を使って説明すると、位置Zから出た光はレンズでZ'で決像され、距離FZ=ｚ、距離F'Z'=z'、レンズの焦点距離をfとすると
-zz' = f^2
という簡単な式で表すことができます。

　たとえば、焦点位置からδだけずれた位置から発した光はどのくらい遠方で決像するかというと、
s = f*f/δ
となりますので、もし焦点距離を100mmとし、δを0.1mmとすると
s = 100*100/0.1 = 100000 mm = 100 m
100m先で決像することがわかります。　δ=0.0mmとすれば、S=∞になることもわかります。
これでδを焦点位置から前後させたのを焦点深度とするとsは被写界深度になることがわかったと思います。

本題に戻ると、デジカメの焦点深度δが決定されれば被写界深度も決まることがわかったところで、その被写界深度内に収まるようなコリメート光学系を用意します。　下の図はデジカメの光路図と思ってください。　またレンズの大きさやカメラ間の距離は遠方sに比べると非常に小さいので、無視。

デジカメの光路図 焦点位置から（前後に）δだけずれた位置からの光がある遠方で決像する図です。　この遠方からの光線とまったく同じ光線を作るには下の図のように焦点位置からεずれたところから光を発すればよいのです。

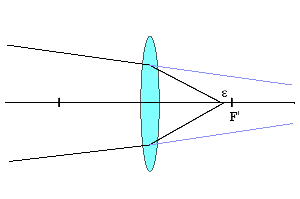焦点位置からεずれた位置から発する光線の様子
このコリメート光学系もまたニュートンの式に当てはまりますから、εとδの関係が求まります。

デジカメの光学系をニュートンの式に当てはめると、
δ/s=-(f1^2)
コリメート光学系も同じようにニュートンの式に当てはめると、
ε/s=-(f2^2)
となり、sが共通しているのでこれら２つの式をまとめると、
ε=δ・(f2/f1)^2
となります。
この式の意味はコリメートする光学系にナイフエッジを置くときの誤差εはデジカメの焦点深度δの(f2/f1)^2　倍で許容されると言うことです。　例えば、デジカメの焦点深度を10ミクロン、焦点距離10mm、コリメートの焦点距離100mmとすれば、ナイフエッジの置く位置の誤差は1mmまで許容されるということです。　ですから、できるだけ焦点距離の長いレンズをコリメートに使うと良いのです。
2001,12,29

Astronomy

TOP

mail