回折格子形状と回折効率
分光計測する際に、回折格子を用いた分光器が使われることが多いです。 回折格子を使ったときに最も注意するべき部分は回折効率です。 回折効率とは何%の割合で光が目的の場所に集中するかを計る量です。 高校物理ではガラスに等間隔の溝を掘ると回折格子ができることを説明し、実際に回折格子のレプリカを使って、太陽や室内灯が虹色に分散させてくれることをしります。 しかし良く見ると、虹だけでなく、光源自体もはっきり見えたり、他の虹も見えたりします。 これは回折格子特有の0次光や1次光の光が見えていることを意味しています。 分光計測ではできるだけ、目的の次数のみの光を使って光の強度を測るのが理想です。
ではどのようにしたら目的の光だけを集めることができるのでしょうか? それには溝の形状を屋根型にする必要があります。 最初に学ぶ回折格子では、溝の間隔が光の射出する角度とその波長にある条件を満たせば、回折が起こることを説明してくれています。 つまり溝を通った光だけが回折するということを言っているのです。 では溝と溝の間を通った光はどうなるのでしょう? 条件を満たさないので、回折に参加できなくなり、よからぬ方向へ飛んでいってしまいます。
溝を屋根型にすることで、すべての光を回折の条件に当てはめることができるます。 これを説明するには波面という考え方を使います。 が、詳しいことは割愛して簡単に説明すると、波面を揃えるだけで全部の光が目的の場所に集中してくれるのです。
しかし、物作りには常に精度の限界がありますので、きっちり屋根型にガラスを加工することはできません。 では一体、どのくらいの形に出来上がれば、どのくらいの効率で回折が起こるのでしょうか? とても興味ある部分です。 実際に計算で物の形と回折効率を見てみることにしましょう。
計算のやり方は、図のように回折格子に白色光を当てます。 回折格子を通った光は色ごとに分散され、長波長の光ほど大きく分散されます。 ある特定の波長ごとにどの角度でどれだけの光がやってくるかを計算するものです。
 計算する光学系の概念図
計算する光学系の概念図
計算条件は以下のとおり
波長 : 400,500,600nm の3波長
溝の深さ : 500nm で最適化
溝の間隔 : 200本/mm
溝本数 : 10本
1つのみぞの分割数 : 30分割
溝が完璧であるケース
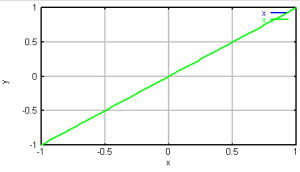
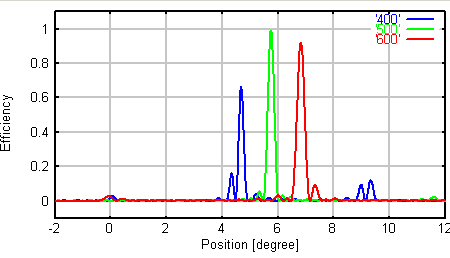 左: 1つの溝の形 、 右 回折効率 (青:400nm、緑:500nm、赤:600nm)
左: 1つの溝の形 、 右 回折効率 (青:400nm、緑:500nm、赤:600nm)
溝の両端でややだれているケース
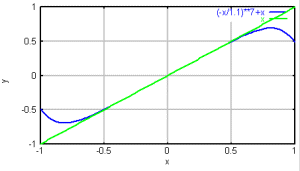
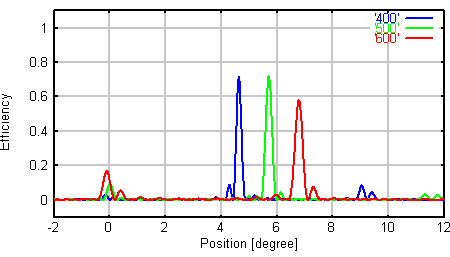 左: 1つの溝の形 、 右 回折効率 (青:400nm、緑:500nm、赤:600nm)
左: 1つの溝の形 、 右 回折効率 (青:400nm、緑:500nm、赤:600nm)
溝の端で大きくだれているケース
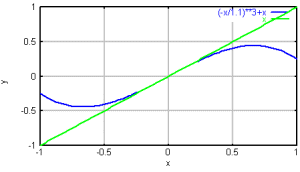
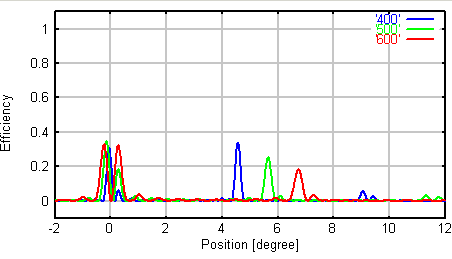 左: 1つの溝の形 、 右 回折効率 (青:400nm、緑:500nm、赤:600nm)
左: 1つの溝の形 、 右 回折効率 (青:400nm、緑:500nm、赤:600nm)
溝の形状がだれていくにしたがって、回折効率が低下していることがわかります。 通常ですと、回折効率が70%前後というのがよく市販されています。 2番目のケースに近いということです。
9,2,2000
Astronomy
Optics
TOP
mail







