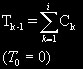個体数の調査方法
タガメやゲンゴロウ等の止水性水生昆虫を対象とした個体数の調査方法 (2006-09-03)
個体数を推定することは生態学的に重要な調査方法のひとつです。ここでは一般的に用いられている3つの手法を解説しますが、特に水生昆虫の調査方法に有用な除去方法に焦点を当て、詳細に説明します。除去方法はあまり一般的ではなく、詳細に解説しているホームページもほとんど無いため、教育・研究用として、あえて除去方法を用いた個体数推定方法を取り上げ、最終的にはWindowsプログラムとして紹介することを目的としました。実際にゲンゴロウやタガメなどの止水性水生昆虫の個体数を調査する際には、目的種、調査地の環境等を考慮の上、適宜選択して頂きたいです。
なお、内容は生物系の大学生以上が対象となりますし、実際にある大学から本内容の一部を教育(生態学の講義)用として使用したいとの依頼があったことを付け加えておきます。そこで、自分の知識の整理も兼ね、本HPで公開することにしました。しかしながら、私自身、生態学者ではないため、誤った記述等、多々あるかと思いますので、メールにてご指導頂けますと幸いです。
1. 区画法(コドラート法:Quadrat Method)
個体数を正確に知るためには、調査地全体の目的生物の個体数をくまなく数えれば良いのですが、広大な調査地を人力で行うには無理があります。そこで、実際には調査地にいくつかの一定の区画(コドラート)を設定し、その中の目的生物の個体数を調べ、区画ごとの密度から全体の個体数を推定する方法です。水生昆虫で言えば、ゲンゴロウのようなため池に生息する種には不向きですが、シャープゲンゴロウモドキ、コオイムシ及びヒメタイコウチのような水深が極めて浅い湿地等に生息する種には、有効な個体数推定方法だと思われます。
2. 標識再捕獲法(Mark and Recapture Method)
採集個体に標識してから放流し(M)、しばらくしてから再度捕獲します。標識された再捕獲個体数(m)が採集個体数(n)のどれだけ含まれているかによって、全個体数(N)を推定する方法です。標識した個体が均一に混ざっていれば、捕獲した際の標識個体も同じ割合で存在することになります。たとえば、100頭(N)のゲンゴロウのうち半分の50頭を取り標識します(M)。つまり、標識率は50%とになります。ゲンゴロウを一旦水槽に戻し、しばらく経ってから、水槽から20頭、無作為にすくいます(n)。標識した個体が均一に混ざっていれば、掬い上げた個体数の半数(10頭)は標識された個体のはずです。つまり、以下の関係が成り立ちます。
| 全個体数(N):再捕獲数(M)=標識放流個体数(n):再捕獲された標識個体数(m) |
よって、推定個体数は、N=n×M/mで表すことができます。個体数を推定する一般的な方法として広く知られ、一番多用されている手法です。深いため池に生息し、移動能力の高いオオゲンゴロウなどは、トラップを用いて行うと良いです。ただし、非標識個体と均一に混ざるまでの時間が必要なこと、飛翔による移動(移入・移出)が無いことが前提となるため、短期間での試験になるかと思われます。この手法を用いることで、多数ある物の数を比較的正確に、早く数えることができます。
例として、碁石の数を推定してみましょう。
100個の碁石(総個体数:N)のうち、20個(M)は標識したと仮定し、白い碁石と取り替えるということにします。この100個の碁石から、無作為に30個を取り(n)、その中に標識したと仮定した白い碁石数(m)を求めます。そして、碁石の総数が100個に近いことを確認する実験を行ってみます。
①黒い碁石を80個取り、外から内部が見えない袋に入れる。
②白い碁石を20個取り(M)、同様に、袋に入れ、黒い碁石と良く混ぜる。
③袋から無作為に30個取り(n)、白の碁石数(m)を数える。
④上記の操作を5回行い、平均値を求める。 |
下表にその結果を示しました。10回の実験の平均推定数は、101.7個となり、実際の総数100個とほぼ同じになりました。もっと実験回数を増やせば、理論上、限りなく100個に近い数値になります。こんな簡単な実験ですが、意外と正確な値が推定できますよ。
| 実験 |
白の碁石数
(m) |
碁石の推定総数
(N) |
| 1 |
6 |
100 |
| 2 |
5 |
120 |
| 3 |
7 |
86 |
| 4 |
6 |
100 |
| 5 |
5 |
120 |
| 6 |
7 |
86 |
| 7 |
5 |
120 |
| 8 |
6 |
100 |
| 9 |
6 |
100 |
| 10 |
7 |
86 |
| 平均値 |
|
101.7 |
3. 除去法(Removal Method)
3-1. 最尤法(Maximum likelihood method)
動物の個体数を推定する手法としては、先に説明した標識再捕獲法が一般的な方法ですが、ほとんど移動しない個体や標識することが困難な個体などは、標識再捕獲法は個体数の推定には妥当ではありません。例えば、水生昆虫の幼虫(ゲンゴロウやタガメなど)は成長の段階で脱皮をします。せっかく標識しても、脱皮の際に標識がなくなってしまいますので、高頻度での調査が要求されます。また、ヒメタイコウチのようにあまり移動しない種も標識再捕獲法は使うことが出来ません(先にも述べたように、標識個体と非標識個体とが均一に混ざることが標識再捕獲法の前提条件のひとつです)。従って、ゲンゴロウ類の幼虫の個体数を推定する方法として、除去法が妥当と考えられます。
除去法には色々な手法があり、調査対象とする生物、場所などによって使い分けされています。 主に用いられている手法を推定理論から分類すると以下の2種類に分けられます。現在使われている手法の多くは、これらを改良した方法で実施されています。その第一の手法として、Moran(1951)が提唱し、Zippin(1956)によって改良された最尤法が良く知られています。これは、全個体群から複数の採集(除去)によってそれぞれの除去された個体数から全体の個体数を推定する手法です。例えば、全個体数が100頭いる湿地帯で採集を開始し、10分の採集で40頭採集したとします(採集した個体はリリースしない)。5分休憩後、次の採集を継続しますが湿地に残った全個体数は既に除去(採集)されたため、60頭となります。当然のことながら、最初の100頭よりも少ない個体から採集を開始するため、個体密度が低く、採集できる個体数は最初よりも確率的に低いと考えられます。すなわち、最初の採集よりも2回目の方が採集個体数は少ないと予想できます。ここで、勘違いしないで頂きたいのは、各採集の条件が同じであれば、採集の回数が増す毎に、採集できる個体数は減っても個体を発見できる確率(発見率)は、理論的に各採集毎に同じです。
2度目の10分間の採集では20頭採集できたとすると、湿地に残った全個体数は40頭となります。このように、同一条件下で3回以上採集し、それぞれの採集時における個体数の減少率から全個体数を推定します。なぜ3回以上なのかというと、統計学的に個体数及び信頼区間を推定するために必要な最小の回数だからです。この調査方法で特に注意したいのは、各調査時の採集条件は常に同じということが前提となります。これは発見率が個体数を推定する上で最も重要なパラメータとなっているからです。最初の調査は3人で実施したのに、2回目の調査では5人で調査したのでは、個体の発見率は当然違ってしまいます。人数が多ければ発見率は高くなります。同様に、最初の調査では直径30cmのネットを使ったのに、次の調査では直径50cmのネットで行ったのでは条件が異なり正しい推定は出来ません。もし、調査ごとに発見率が変わることが想定されるような場合には、別の手法を用いることになりますが、ここではその方法に関しては省略します。それでは最尤法として、Zippinの手法を解説します。
個体数(N)と発見率(p)は、以下の数式で推定できます(Zippin, 1956)。

で求めることが出来ます。
除去採集のデータを上記の計算式に入力すれば、Rが算出できます。Zippinの原著論文(1956)の図2の関数から、そのR(縦軸)の値に相当する1-qs(横軸)を肉眼で読み取ります。かなりアバウトで面倒な方法のため、プログラム化することを前提に、原著の図2を高次関数として置き換えることにしました(数学的には、別の関数(才尤関数)を用いるべきところですが、Zippinの論文の図から数値を読み取るのであれば、むしろ当てはめた単純な高次関数から概算値を算出する方がプログラミングする上では簡便と判断しました)。この論文では、サンプリング回数(S)は3、4、5及び7に限定されておりますので、この4パターンに関して当てはめた関数及び図は以下のようになりました。なお、プロットした点は、Zippinの論文より読み取った値です。
なお、95%信頼区間とは、100回調査した時、95回の調査における推定値はこの区間に収まると言う確率を示しております。よって、95%信頼区間がより小さければ、それだけ正確な推定値が得られたことを意味します。
S=3の時
y = -6.3554x5 + 12.977x4 - 9.5227x3 + 2.5424x2 - 0.4288x + 1.0016
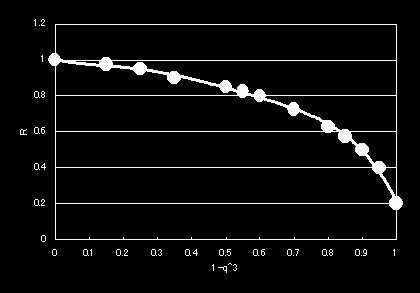
S=4の時
y = -7.0653x5 + 12.881x4 - 8.0369x3 + 1.4297x2 - 0.3028x + 1.5014
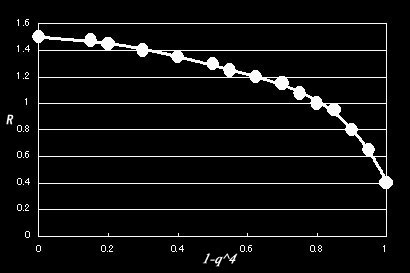
S=5の時
y = -68.086x6 + 185.23x5 - 190.82x4 + 90.848x3 - 19.913x2 + 1.1655x + 1.9968
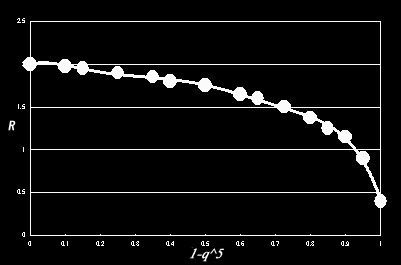
S=7の時
y = -42.846x6 + 112.44x5 - 116.38x4 + 59.324x3 - 15.938x2 + 1.3769x + 2.9169
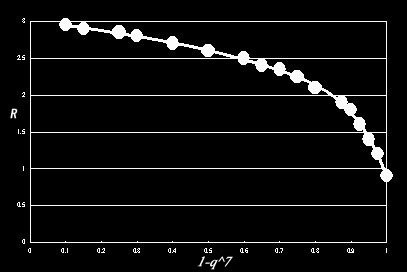
となります。
後ほど、実例を用いて計算してみます。
3-2. 直線回帰法(Linear regression method)
除去法の第二の手法として、Hayne(1949)が提唱した直線回帰法による推定です。最尤法に比べて理論が容易なため、よく用いられている推定方法です。

調査回数iに関して、これまでに除去採集した総個体数をTi、その時点から次の調査i+1までの捕獲数をCiとすると、除去方法が成立する前提条件のもとで採集した場合、CiとTiの間には直線関係が成り立ちます。i回の除去採集を行ったとすると、それまでの累積捕獲数は、以下の式で表すことができます。
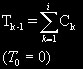
縦軸に捕獲数(Ci)、横軸にこれまでの総捕獲数(Ti)をプロットすると、図1のような傾き負の直線となります。この直線の傾きをa、y切片をbとすると、Ci=-aTi+bという式になります。この直線がx軸と交差する点が推定個体数となります。従いまして、CiとTiのいくつかのデータセットがあれば、推定個体数(N)は容易に計算できるはずです。すなわち、Ci=0の時のTiの値がNとなるわけです。上記の式のCiにゼロを代入し、Ti=b/a、つまり、N=b/aとなります(回帰直線を求め、y切片の値を傾きの絶対値で割れば推定個体数が計算できます)。また、95%信頼区間は、最尤法と同様、N±√1.96
で求められますが、ここでは、より正確な方法(2次方程式を用いた手法)で計算するようにプログラムに組み込みました。その詳細な理論は、Seber(1982)の文献を参照してください。
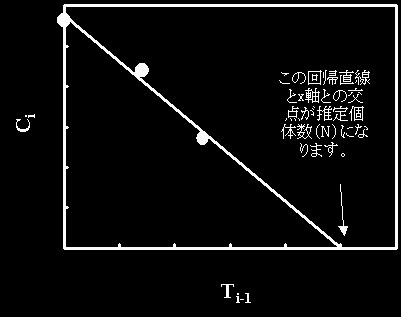 |
| 図1 直線回帰法を用いた個体数推定。捕獲数とこれまでの総捕獲数との関係 |
では、実際に上記で解説した2種類の除去法によって個体数推定のモデル実験を行ってみましょう。標識再捕獲法では碁石を用いたましたが、今回はマイクロチューブ(容量3mL)を使って行いました。マイクロチューブとは、生物研究によく用いられるプラスチック製の小型試験管です。
今回の実験目的は、以下の4つです。
① 個体数推定のPC用プログラムの使用方法を学ぶ。
② 最尤法及び直線回帰法の2種類の除去法で、両者の違いを確認する。
③ 採集力が異なった場合の推定個体数の違いを確認する。
④ 上記の結果から、除去方法を行う上での留意点を考察する。 |
実験は手の大きさ(親指先端から小指先端までの長さ)が違う3人で行いました。ちなみにTは筆者、Yは妻、Aは娘です。手の大きさはは筆者が一番大きく(21cm)次いで妻(17cm)、幼稚園児の娘(12cm)です。当然のことながら、大きい手の方が、よりたくさんのマイクロチューブを一掴みでつかめるはずです。すなわち、手の大きさの違いが、採集力の違いとなります。もっとわかり易く言うと、「手の大きさ=網の大きさ」に置き換えることが出来ます。同じ努力量であれば、大きな網(大きな手)の方が、より多くの個体を捕らえることが出来ます。マイクロチューブをつかむ行為が採集することに相当します。
「全個体数 = マイクロチューブの総数」
「一定時間の採集 = ひと握りのマイクロチューブ採取」
マイクロチューブ100個を準備する。マイクロチューブが調査する個体と仮定する。
① 100個のマイクロチューブを袋か箱に入れ、その中からひと握りだけのマイクロチューブを取り出す(網を使って一定時間採集したと仮定)。
② 取り出したマイクロチューブの数を数える(1回目の調査個体数)。このマイクロチューブは戻さない。
③ 次に、残ったマイクロチューブから再度、ひと握りのマイクロチューブを取り出す(2回目の採集調査)。
④ 取り出したマイクロチューブの数を数える(2回目の調査個体数)このマイクロチューブも戻さない。
⑤ 再度、残ったマイクロチューブからひと握りのマイクロチューブを取り出し、数を数える(3回目の調査個体数)。
⑥ これで、3回の除去採集を行ったとする。
⑦ 上記の操作を最初から5回繰り返す。 |
結果は表1~3に示しました。
表1. 実験者:T(筆者)、手の大きさ:21cm
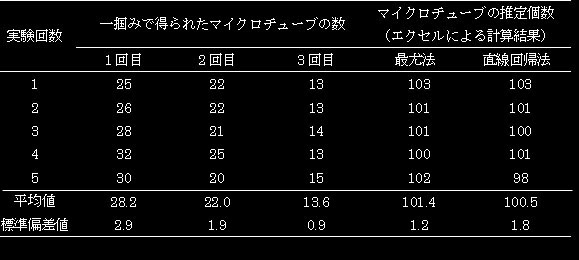
表2. 実験者:Y(妻)、手の大きさ:17cm
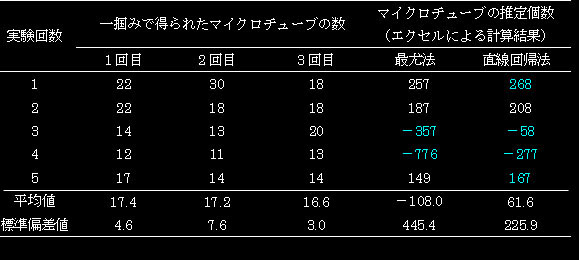
表3. 実験者:A(娘)、手の大きさ:12cm
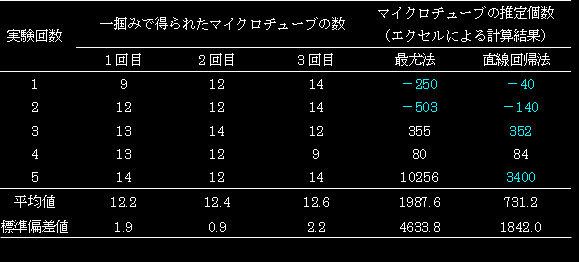
青字は入力データが除去法に不適切のため、後述するプログラムでは算出できません。
4. 個体数推定法のWindows対応プログラム
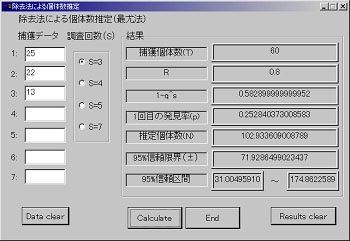
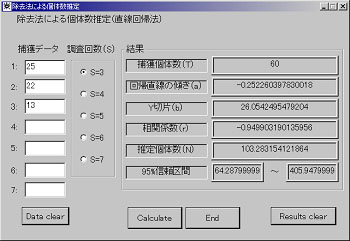
表1~3の結果を説明する前にWindowsプログラムの使用方法を述べたいと思います。プログラムのアルゴリズムや計算理論は、先に説明した通りです。まず、各プログラムを自分のPCにダウンロードする必要があります。このページの最後の方にダウンロード法を指示してありますので、各自、ダウンロードしてください。それぞれのプログラムを起動すると、最尤法の場合は図2、直線回帰法は図3の画面が現れます。
データを入力する箇所は、左側の「捕獲データ」及び「調査回数(S)」だけです。例えば、表1の実験1のデータ(25、22、13)を例にすると、捕獲データ及び調査回数を入力しますが、調査回数は捕獲データの数と同じでなければいけません。今回の例では、3回の調査のため、調査回数は3を選択します。そして、Calculateボタンを押せば結果が表示されます。その際、調査回数を4とした場合、捕獲データは(25、22、13、0)と認識され、結果は異なりますので気を付けてください。同様に、調査回数を5にすると、捕獲データは(25、22、13、0、0)として計算されます。入力データ及び結果のみを消去する場合は、それぞれData
clear、Results clearのボタンを押します。また、プログラムを終了する場合はEndボタンを押してください。一つ注意して欲しいのは、うまく除去採集出来ていないデータ等を入力した場合、それを回避する命令を組み込んでいないため、プログラムはフリーズします。表2~3の青字で示した結果は本プログラムでは算出できません。その場合、ウィンドウの×等を押し、強制終了してください。また、PCの性能によっては計算に時間がかかります。表1~3の例題等で色々と試して下さい。
 |
 |
| 図2 才尤法を用いた個体数推定 |
図3 直線回帰法を用いた個体数推定 |
それでは、先に行った実験結果(表1~3)を解説します。皆さんも、プログラムを使用しながら読んで頂けると理解しやすいかと思います。
表1では1回目の採取で平均約28個のチューブをつかむことができましたが、2回目には22個、3回目には14個というように採取の回数が増すごとにつかむことの出来るチューブの個数が減少していきます。これは、3回の除去採取によって、全個数からうまく除去されていることを示しております。また、同じ実験を5回繰り返しましたが、エクセルという表計算ソフト(マイクロソフト社)を用いて、直線回帰法によって算出した推定個数は、5回実施したそれぞれの試験でほぼ100個に近いことも確認することができました。
表2のデータは、結果1よりも手のサイズがやや小さい人が行いました。3回の連続した除去採取によって、5回の平均値から見ても、1回の採取で約17個の一定数しか除去できていません。すなわち、全個数からうまく除去採取できていないようです。また、反対に1回目の採取よりも3回目の採取の方が、つかんだ個数が多い例もあり(実験回数3)、エクセルで推定した個数がマイナスとなることもありました。これは、チューブの総数が多すぎ、採取能力(つかむ能力)が低いため、連続した3回の除去採取では、全体からうまく除去できていなためと考えられます。こう言った場合は、採取能力を上げるか、連続した除去採取の回数を増やすなどして、全体から除去できるような採取系を検討する必要があります。
表3のデータも結果2と同様に、全体から上手く除去採取できていない事例です。採取能力に比べて、総数が多すぎるため、除去できておりません。極端に表現すると、太平洋の真中で、たった一人、小さいタモ網でニシンの大群をすくうようなものですね。
このように、除去方法は調査対象とする全個体数と採集能力とのバランス関係が重要なため、正確な個体を推定するには予備試験等を実施し、採集方法など、十分吟味し実施することが大切だと思います。では「上手く除去採集できたか」と言う判断基準は無いのか、と質問が出ると思います。予備試験を実施するにもある程度の判断基準があれば、実験者としては嬉しいはずです。そこで、調査の妥当性を上記の実験結果を用いて客観的に知る方法を述べたいと思いますが、最尤法と直線回帰法とではその方法が若干異なります。しかしながら、除去法の性質上、連続した各調査時における発見率はどちらの採集法も同一であるはずです。従って、発見率が推定個体数を決定する大きな要因であると考えることが出来ます。才尤法の発見率は何度も出てきましたが、pとして算出できます。直線回帰法は、図1のような右下がりの直線となります。つまり、一定の割合で全個体数から除去されています。この直線の傾きの絶対値こそが発見率を表しております。そこで、才尤法の発見率(p)と直線回帰法の傾き(a)及び相関係数(r)との関係を表1~3のデータから比較したいと思います。皆さんもプログラムを使って実際に確認してみてください。結果は表4に示しました。
表4 最尤法の発見率と直線回帰法の傾き及び相関係数並びに本プログラムによる計算の可否
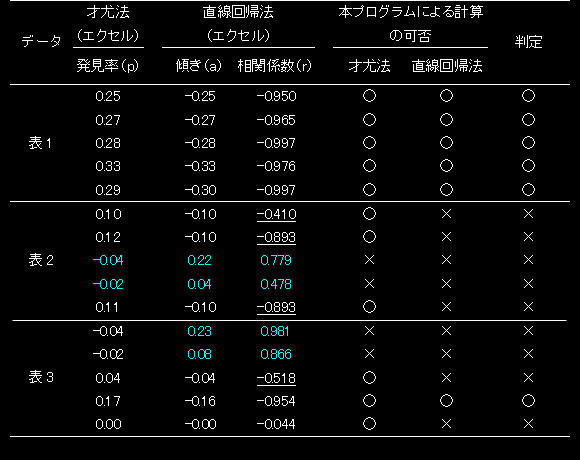
表中の青字は、除去法において不適切なパラメータ(発見率が負、傾きが正、相関係数が正)を示した。また、下線のある数字は、相関係数が-0.95~-1.00以外の値を示した。○と×は、それぞれ、可と否を示す。
表1のデータは、既に述べているとおり、除去採取がうまくいった例です。最尤法の発見率(p)と直線回帰法の傾き(a)の絶対値が一致しました。また、表2及び表3のデータに関しては、表4の白字で示したように、最尤法で発見率が正の値を示した試験においては、直線回帰法の傾きの絶対値と一致しております。すなわち、先に述べたとおり、直線回帰法の発見率は、理論的に回帰直線の傾きの絶対値に相当します。また、相関係数(r)は、限りなく-1に近いのが望ましいです。ところが、青字で示した箇所は、先にも説明した通り、除去採取がうまく行っておらず、才尤法においては発見率が負の値を示し、直線回帰法においては傾きが正の値を示しております。これでは、正確な推定値が求まりません。しかしながら、才尤法で発見率が正の値を、直線回帰法で傾きが負の値をそれぞれ示したとしても、直線回帰法においてrが悪ければ、直線性が担保されません。表4の下線をひいた数字はrが悪く(-0.95~-1.00以外)、他のパラメータが良好であっても正確な推定値は求まりません。一つの基準として、rが-0.95~-1.00を示したデータは、比較的、真の値に近いと考えることが出来ます。従いまして、除去採集が的確に行われたかの判断としては、下記の3つを満たすことが一つの目安になると思われます。
① 才尤法において、発見率(p)が正の値を示す。
② 直線回帰法において、回帰直線の傾き(a)が負の値を示す。
③ 直線回帰法において、相関係数(r)が-0.95~-1.00を示す。 |
本プログラムでは、それぞれの条件を満たさないとフリーズしますので、除去採集の妥当性を知る一つの指標になるかと思います。表4において、この条件を満たしたものを判定として○(可)と×(否)で表記しました。
より理解を深めるため、具体的に直線回帰方法を例に説明します。既に解説した通り、直線回帰方法は、除去採取された個数を積算していくため、その直線の傾きが個数を推定するための重要なファクターであると考えられます。図1で示したように直線回帰法を用いた個体数推定は、捕獲数とこれまでの総捕獲数との関係で示されるため、右下がりの直線となります。つまり、傾きが負の直線となると考えられます。表1の平均データを直線回帰法に従ってグラフにすると図4になります。同様に、表2、3については図5及び6となります。
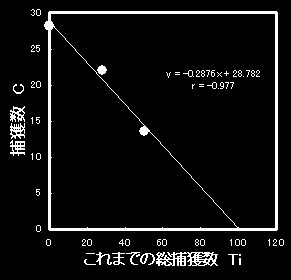
表1のデータは最尤法では、比較的よく当てはまっていると述べましたが、直線回帰法においても直線の傾きから判断すると、きれいに除去採取されていることがわかります(比例的に減少→各採集時の発見率は同じ)。また、rが-0.977となり、良好な線形性が保たれていることがお分かりいただけると思います。
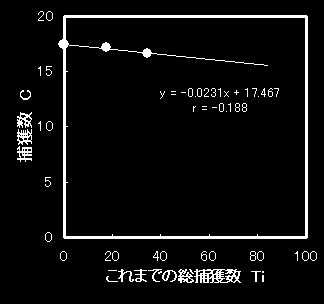
表2のデータを直線回帰法で表すと、図5の通り、なだらかな右下がりの直線にはなっておりますが(従って、推定値は実測値よりもはるかに大きくなる)、rが-0.188と直線性が保たれておりません。
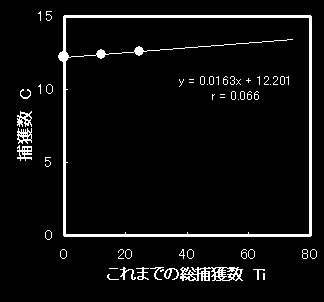
また、表3の結果を直線回帰法で示すと(図6)、右上がりの直線となり、rも0.066と直線性が全くありませんでした。先に図1で説明した通り、回帰直線の延長線がx軸と交わる箇所が推定個数なため、図6からでは、理論上、x軸と交わることがなく、プログラム上、エラーとなります。
当然、推定値は算出できなくなります(とんでもない値を返します)。従いまして、直線回帰法にて除去法を実施する場合、捕獲数(Ci)とこれまでの総捕獲数(Ti)の関係式から相関係数(r)を求め、できるだけrが-1に近づくデータが理想といえます。
 |
 |
 |
| 図4 表1のデータを直線回帰法で作図 |
図5 表2のデータを直線回帰法で作図 |
図6 表3のデータを直線回帰法で作図 |
以上のことから、除去法を行った場合のデータの妥当性は、以下のことを目安にすると良いです。
① 才尤法と直線回帰法の両方で実施する。
② 才尤法の発見率(p)が正の値を示す。
③ 直線回帰法の傾き(a)の絶対値が負の値を示す。
③ ②と③の値がほぼ同じ。
④ 直線回帰法の相関係数(r)が、-0.95~-1.00を示す。 |
以上、除去方法のデータから、そのデータの妥当性を評価する方法を解説しましたが、これらはあくまでも目安に過ぎません。
5. ダウンロード
対応システムは、Windowsマシンのみです。OSはWindowsXP、2000、NT4.0、Me、95で動作確認済みです。ZIPファイルを解凍後、Removal
Methodという実行ファイルを起動するとフォルダーが作られます。その中に下記の2つのプログラムが入っています。ただし、パスワードを入力しないと解凍が出来ません。このプログラムを使ってみたい方はメールでその旨お知らせ頂ければパスワードをお教えいたします。バグもあると思われますし、使ってみて推定値が正確でない場合や不都合なこと、要望等、是非、ご指摘頂けますと幸いです。今後の改良の参考にしたいと思っています。
ファイル名:「Removal Method.zip」 (18.6KB) ⇒ 
解凍後、以下の2つのファイルができます。
①「除去法による個体数推定:直線回帰法」ファイル名:RM_Reg
②「除去法による個体数推定:最尤法(Zippin法)」ファイル名:RM_Zippin
なお、本プログラムを使用して生じた如何なる不利益に対しても、作者は責任を持ちません。各個人の責任でご自由にお使いください。また、フリーソフトですが、その権利を放棄したわけではありません。本プログラムの内容や本プログラムを使って得た結果(副産物)を無断で他に引用、転記、公表することはご遠慮ください。また、営利目的での使用は固くお断りします。教育、研究、あるいは調査の参考程度にお使い下さい。
6. 参考文献
① 伴幸成・柴田茂昭・石川雅宏(日本の昆虫⑭ヒメタイコウチ、文一総合出版)
② 久野英二(動物の個体群動態研究法Ⅰ、共立出版)
③ Moran (1951) A mathematical theory of animal trapping. Biometrika. 38: 307-311.
④ Hyne (1949) Two methods for estimating population from trapping records. J. Mamm. 30: 399-411.
⑤ Zippin (1956) An evaluation of the removal method of estimating animal
populations. Biometrics. 163-169.
⑥ Seber(1982)The estimation of animal abundance and related parameters,
2nd edition, London: Charles Griffin and Company Limited.